a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} - 4x + 3,y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Lập bảng biến thiên của hàm số:
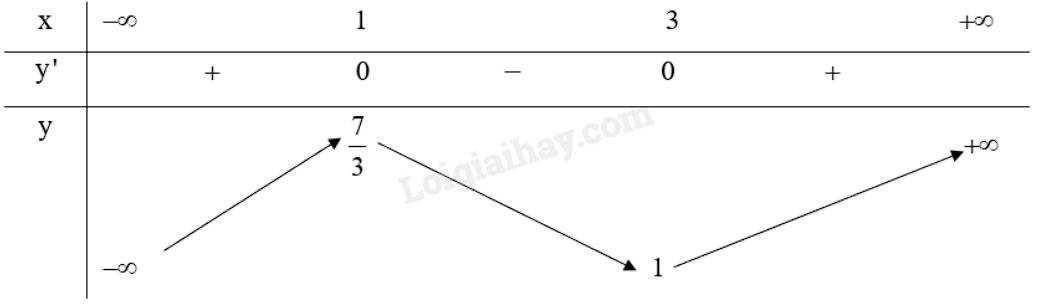
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) nghịch biến trên khoảng \(\left( {1;3} \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 4x - 5\)
Vì \( - 3{x^2} + 4x - 5 = - 3\left( {{x^2} - 2.\frac{2}{3} + \frac{4}{9}} \right) - \frac{{11}}{3} = - 3{\left( {x - \frac{2}{3}} \right)^2} - \frac{{11}}{3} < 0\;\forall x \in \mathbb{R}\)
Do đó, \(y' < 0\;\forall x \in \mathbb{R}\).
Vậy hàm số \(y = - {x^3} + 2{x^2} - 5x + 3\) nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).


