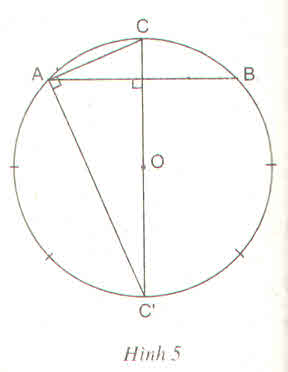
Hình a.
Gọi ai là cạnh của đa giác đều i cạnh.
a) a6= R (vì OA1A2 là tam giác đều)
Cách vẽ: vẽ đường tròn (O;R). Trên đường tròn ta đặt liên tiếp các cung 
, 
,..., 
mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
b) Hình b
Trong tam giác vuông OA1A2: a2 = R2 + R2 = 2R2 => a4 = R√2
Cách vẽ như ở bài tập 61.
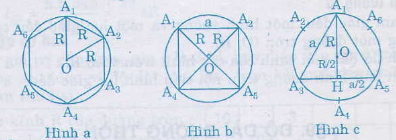
c) Hình c
A1H = R + =
A3H =
A1A3 = a
Trong tam giác vuông A1HA3 ta có: A1H2 = A1A32 – A3H2.
Từ đó = a2 -
.
=> a2 = 3R2 => a = R√3
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác A1A3A5 như trên hình c
Hình a.
Gọi ai là cạnh của đa giác đều i cạnh.
a) a6= R (vì OA1A2 là tam giác đều)
Cách vẽ: vẽ đường tròn (O;R). Trên đường tròn ta đặt liên tiếp các cung , ,..., mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
b) Hình b
Trong tam giác vuông OA1A2: a2 = R2 + R2 = 2R2 => a4 = R√2
Cách vẽ như ở bài tập 61.
c) Hình c
A1H = R + =
A3H =
A1A3 = a
Trong tam giác vuông A1HA3 ta có: A1H2 = A1A32 – A3H2.
Từ đó = a2 -
.
=> a2 = 3R2 => a = R√3
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác A1A3A5 như trên hình c
