
Nhìn vào đồ thị, ta thấy:
a) Hàm số \(y = - 2x + 1\)nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)

Nhìn vào đồ thị, ta thấy:
a) Hàm số \(y = - 2x + 1\)nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
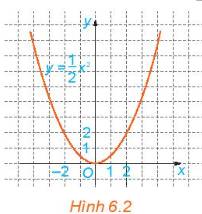
a) Dựa vào đồ thị của hàm số \(y=\dfrac{1}{2}x^2\)(H.6.2), tìm \(x\) sao cho \(y=8\).
b) Vẽ đồ thị của các hàm số \(y=2x+1\) và \(y=2x^2\) trên cùng một mặt phẳng tọa độ.
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
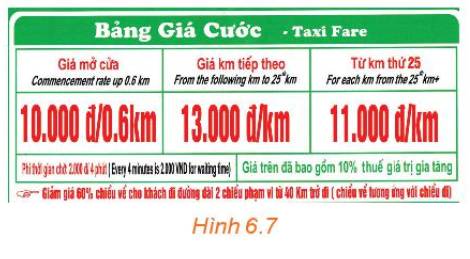
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Tìm tập xác định của các hàm số sau:
a) \(y=2x^3+3x+1\);
b) \(y=\dfrac{x-1}{x^2-3x+2}\) ;
c) \(y=\sqrt{x+1}+\sqrt{1-x}\).
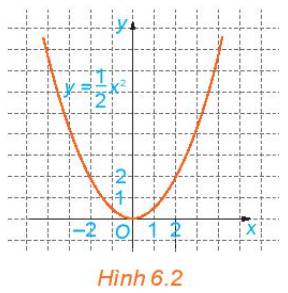
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y=\dfrac{1}{2}x^2\).
\(\left(0;0\right);\left(2;2\right);\left(-2;2\right);\left(1;2\right);\left(-1;2\right)\)
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
Cho các hàm số \(y=-x+1\) và \(y=x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=-x+1\) | ? | ? | ? | ? | ? |
| \(y=x\) | ? | ? | ? | ? | ? |
Khi giá trị \(x\) tăng, giá trị \(y\) tương ứng của mỗi hàm số \(y=-x+1\) và \(y=x\) tăng hay giảm?
Quan sát đồ thị của hàm số \(y=f\left(x\right)=-x^2\) trên \(R\) (H.6.5).
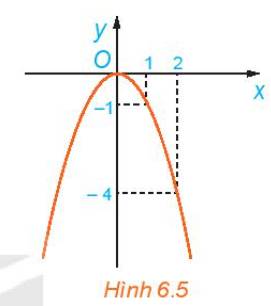
Hỏi:
a) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(-\infty;0\right)\)?
b) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(0;+\infty\right)\)?
Tìm tập xác định và tập giá trị của mỗi hàm số sau:
a) \(y=2x+3\);
b) \(y=2x^2\).
Xét hai đại lượng \(x;y\) phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì \(y\) là hàm số của \(x\)?
a) \(x+y=1\);
b) \(y=x^2\);
c) \(y^2=x\);
d) \(x^2-y^2=0\).