Question

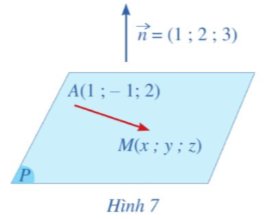
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1; – 1; 2) và có vectơ pháp tuyến là \(\overrightarrow{n}=\left(1;2;3\right)\).

Giả sử M(x; y; z) là một điểm tùy ý thuộc mặt phẳng (P) (Hình 7).

a) Tính tích vô hướng \(\overrightarrow{n}.\overrightarrow{AM}\) theo x, y, z.

b) Tọa độ (x; y; z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0 hay không?

Answer 1

a) \(\overrightarrow {AM} = (x - 1;y + 1;z - 2)\).

\(\overrightarrow n .\overrightarrow {AM} = (x - 1) + 2(y + 1) + 3(z - 2) = x + 2y + 3z - 5\).

b) Tọa độ (x;y;z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0.