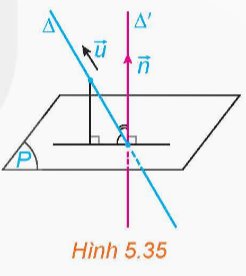
Trong không gian Oxyz, cho đường thẳng Δ và mặt phẳng (P). Xét \(\overrightarrow{u}\) = (a; b; c) là một vectơ chỉ phương của Δ và \(\overrightarrow{n}\) = (A; B; C) (với giá D') là một vectơ pháp tuyến của (P). (H.5.35)
a) Hãy tìm mối quan hệ giữa các góc (Δ, (P)) và (Δ, Δ').
b) Có nhận xét gì về mối quan hệ giữa sin(Δ, Δ') và \(\left|\cos\left(\overrightarrow{u},\overrightarrow{n}\right)\right|\).
a) Mối quan hệ của góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\) là: \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right)\)
b) Ta có: +) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) \le {90^o}\)
+) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left[ {{{180}^o} - \left( {\overrightarrow u ,\overrightarrow n } \right)} \right] = - {90^o} + \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) > {90^o}\)
Suy ra, \(\sin \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).


