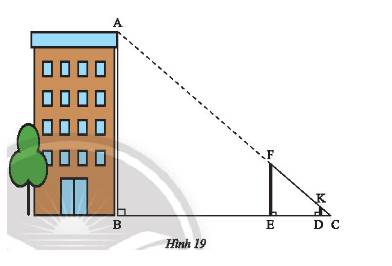
Trên một tờ giấy kẻ cảo có các đường kẻ ngang song song và cách đều nhau.
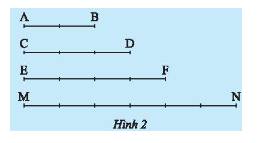
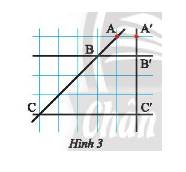
a) Vẽ một đường thẳng \(d\) cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\).
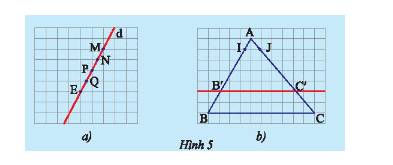
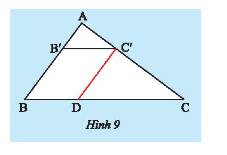
b) Vẽ một tam giác \(ABC\) rồi vẽ một đường thẳng song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) lần lượt tại \(B'\) và \(C'\). Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo tính tỉ số \(AB'\) và \(BB'\); trên cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo tính tỉ số \(AC'\) và \(C'C\) (Hình 5b).
So sánh các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\);\(\frac{{AB'}}{{B'B}}\) và \(\frac{{AC'}}{{C'C}}\);\(\frac{{B'B}}{{AB}}\) và \(\frac{{C'C}}{{AC}}\).
a) Độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau vì chúng đều bằng độ dài đường chéo của một hình vuông nhỏ.
b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).
Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);
Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).
Do đó, \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).
Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).
Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).