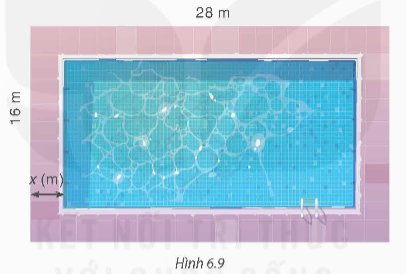
Theo bài, ta có điều kiện của $x$ là $0<x<8$.
Chiều dài của bể bơi là: $28-x-x=28-2 x(m)$.
Chiều rộng của bể bơi là: $16-\mathrm{x}-\mathrm{x}=16-2 \mathrm{x}(\mathrm{m})$.
Diện tích của bể bơi theo x là:
$$
S=(28-2 x)(16-2 x)=448-56 x-32 x+4 x^2=4 x^2-88 x+448\left(m^2\right)
$$
Theo bài, $S=288 \mathrm{~m}^2$ nên ta có phương trình: $4 \mathrm{x}^2-88 \mathrm{x}+448=288$.
Giải phương trình:
$$
\begin{aligned}
& 4 x^2-88 x+448=288 \\
& 4 x^2-88 x+160=0 \\
& x^2-22 x+40=0
\end{aligned}
$$
Phương trình trên có $\mathrm{a}=1 ; \mathrm{b}^{\prime}=-11 ; \mathrm{c}=40$ và $\Delta^{\prime}=(-11)^2-1.40=81$ nên $\sqrt{\Delta^{\prime}}=\sqrt{81}=9$ Do đó, phương trình trên có hai nghiệm phân biệt $x=\frac{11+9}{1}=20$ và $x=\frac{11-9}{1}=2$.
Ta thấy chỉ có $x=2$ thỏa mãn điều kiện $0<x<16$.
Vậy bề rộng của đường đi là 2 mét để diện tích của bể bơi là 288 m².