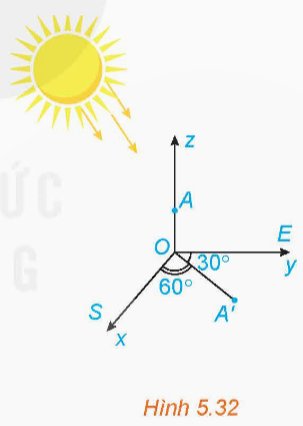
Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6 m vuông góc với mặt đất, có chân cột đặt tại ví trí O trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3 m về hướng S60°E (hướng tạo với hướng nam góc 60° tạo với hướng đông góc 30°) (H.5.32). Chọn hệ trục Oxyz có gốc tọa độ là O, tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.
Ta có: \(A\left( {0;0;6} \right),A'\left( {\frac{3}{2};\frac{{3\sqrt 3 }}{2};0} \right)\) nên \(\overrightarrow {AA'} \left( {\frac{3}{2};\frac{{3\sqrt 3 }}{2}; - 6} \right) \Rightarrow \frac{1}{3}\overrightarrow {AA'} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - 2} \right)\)
Đường thẳng AA’ đi qua điểm \(A\left( {0;0;6} \right)\) và nhận \(\frac{1}{3}\overrightarrow {AA'} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - 2} \right)\) làm vectơ chỉ phương nên phương trình tham số của đường thẳng AA’ là: \(\left\{ \begin{array}{l}x = \frac{1}{2}t\\y = \frac{{\sqrt 3 }}{2}t\\z = 6 - 2t\end{array} \right.\) và phương trình chính tắc là \(\frac{x}{{\frac{1}{2}}} = \frac{y}{{\frac{{\sqrt 3 }}{2}}} = \frac{{z - 6}}{{ - 2}} \Rightarrow \frac{{2x}}{1} = \frac{{2\sqrt 3 y}}{3} = \frac{{z - 6}}{{ - 2}}\).


