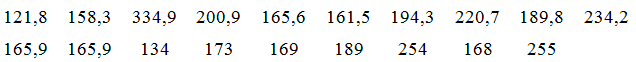a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
Số trung bình của số liệu là: \(\bar x \approx 192,41\)
Tứ phân vị thứ nhất là: \({x_5} = 165,6\)
Tứ phân vị thứ hai là: \({x_{10}} = 173\)
Tứ phân vị thứ ba là: \({x_{15}} = 220,7\)
Giá trị xuất hiện nhiều nhất là \({M_O} = 165,9\)
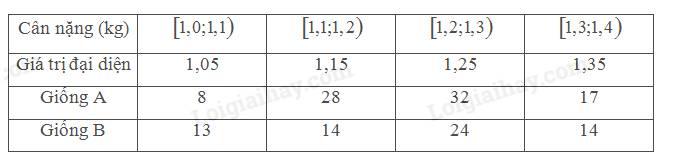
b)
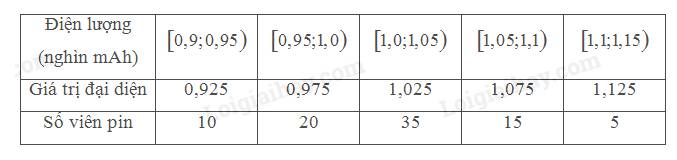
c) Ta có:

• Lượng mưa trung bình trong tháng 8 là:
\(\bar x = \frac{{10.147,5 + 5.202,5 + 3.257,5 + 1.312,5}}{{19}} \approx 188,03\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\).
Do đó: \({u_m} = 120;{n_{m - 1}} = 0;{n_m} = 10;{n_{m + 1}} = 5;{u_{m + 1}} - {u_m} = 175 - 120 = 55\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{120 - 0}}{{\left( {120 - 0} \right) + \left( {120 - 5} \right)}}.55 \approx 148,09\)
• Gọi \({x_1};{x_2};...;{x_{19}}\) là lượng mưa trong tháng 8 được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}}\end{array};{x_{11}},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {175;230} \right)}\end{array};{x_{16}},{x_{17}},{x_{18}} \in \begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array};{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {285;340} \right)}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{10}}\)
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_{10}} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{2} - 0}}{{10}}.\left( {175 - 120} \right) = 172,25\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_5}\).
Ta có: \(n = 19;{n_m} = 10;C = 0;{u_m} = 120;{u_{m + 1}} = 175\)
Do \({x_5} \in \begin{array}{*{20}{l}}{\left[ {120;175} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 120 + \frac{{\frac{{19}}{4} - 0}}{{10}}.\left( {175 - 120} \right) = 146,125\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{16}}\).
Ta có: \(n = 19;{n_j} = 3;C = 10 + 5 = 15;{u_j} = 230;{u_{j + 1}} = 285\)
Do \({x_{16}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {230;285} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 230 + \frac{{\frac{{3.19}}{4} - 15}}{3}.\left( {285 - 230} \right) = 216,25\)