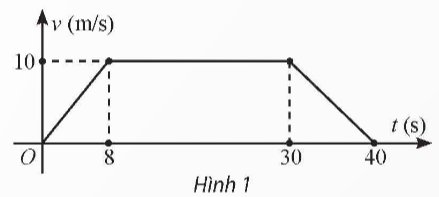
Đồ thị hàm số \(v\left( t \right)\) được chia thành 3 đường thằng \(OA\), \(AB\), \(BC\) như hình dưới đây.

Đường thẳng \(OA\) đi qua \(O\left( {0;0} \right)\) và \(A\left( {8;10} \right)\) nên phương trình đường thẳng \(OA\) là \(v = \frac{5}{4}t\).
Đường thẳng \(AB\) đi qua \(A\left( {8;10} \right)\) và \(B\left( {30;10} \right)\) nên phương trình đường thẳng \(AB\) là \(v = 10\).
Đường thẳng \(BC\) đi qua \(B\left( {30;10} \right)\) và \(C\left( {40;0} \right)\) nên phương trình đường thẳng \(BC\) là \(v = - t + 40\).
Vậy \(v\left( t \right) = \left\{ \begin{array}{l}\frac{5}{4}t{\rm{ }}\left( {0 \le t \le 8} \right)\\10{\rm{ }}\left( {8 \le t \le 30} \right)\\ - t + 40{\rm{ }}\left( {30 \le t \le 40} \right)\end{array} \right.\).
Do đó, quãng đường ca nô đi được trong 40 giây là
\(s = \int\limits_0^{40} {v\left( t \right)dt} = \int\limits_0^8 {v\left( t \right)dt} + \int\limits_8^{30} {v\left( t \right)dt} + \int\limits_{30}^{40} {v\left( t \right)dt} = \int\limits_0^8 {\frac{5}{4}tdt} + \int\limits_8^{30} {10dt} + \int\limits_{30}^{40} {\left( { - t + 40} \right)dt} \)
\( = \frac{5}{4}\left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^8 + 10\left. {\left( t \right)} \right|_8^{30} + \left. {\left( { - \frac{{{t^2}}}{2} + 40t} \right)} \right|_{30}^{40} = \frac{5}{4}.32 + 10.22 + 50 = 310\) (m).
Đáp án đúng là C