thể tích hình chóp đều là
V=\(\dfrac{1}{3}S.H=\dfrac{1}{3}6.4=8\left(cm^3\right)\)
ĐS V=8cm3
Thể tích hình chóp tam giác đều đó là :
\(V=\dfrac{1}{3}.S.h=\dfrac{1}{3}.6.4=8\) (cm)
KL : ....
Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 3cm, đáy 4cm
a) Tính diện tích xung quanh
b) Diện tích toàn phần
c) Thể tích hình chóp
Xét các hình sau :
1) Kim tự tháp Kê - ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m , chiều cao hình chóp 146,5m
a) Độ dài cạnh bên là bao nhiêu ?
b) Tính diện tích xung quanh của hình chóp
c) Tính thể tích hình chóp
2) Kim tự tháp Lu - vrơ (Louvre) (Xây dựng vào năm 1988)
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo thàng Lu - vrơ (Pháp). Mô hình có hạng hình chóp đều chiều cao 21m, độ dài cạnh đáy là 34m
a) Cạnh bên của hình chóp là bao nhiêu ?
b) Tính thể tích hình chóp ?
c) Tính tổng diện tích các tấm kính để phù lên hình chóp này (\(S_{xq}\))
Tính diện tích toàn phần của các hình chóp đều sau đây :
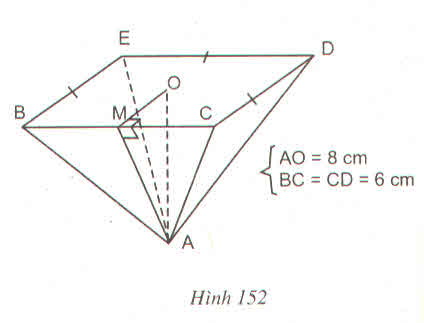
a) Hình cho theo các kích thước trên hình 152
b) Hình chóp tứ giác đều, cạnh đáy 6cm, chiều cao hình chóp 5cm
c) Hình chóp tứ giác đều, cạnh đáy 20cm, chiều cao hình chóp 7cm
d) Hình chóp tứ giác đều, cạnh đáy 1m, chiều cao hình chóp 50cm
Cho hình chóp tứ giác đều có độ dài cạnh đáy là 28m, trung đoạn là 40m. Tính diện tích xung quanh và thể tích hình chóp?
S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua 6 đỉnh của đáy), HM = 12 cm (h.133), chiều cao SH = 35cm. Hãy tính :
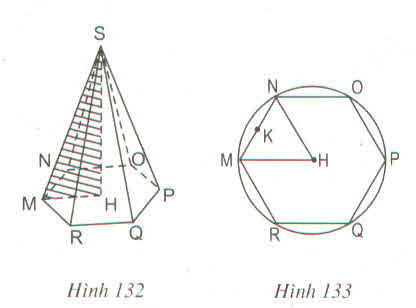
a) Diện tích đáy và thể tích của hình chóp (biết \(\sqrt{108}\approx10,39\))
b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết \(\sqrt{1333}\approx36,51\) )
Cho hình chóp cụt tứ giác đều \(ABCD.A_1B_1C_1D_1\) có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm. Hãy tính :
a) Diện tích xung quanh của hình cụt
b) Tính cạnh bên và chiều cao của hình chóp cụt
a) Tính thể tích của hình chóp đều (h.136)
b) Tính diện tích xung quanh của hình chóp cụt đều (h.137)
(Hướng dẫn : Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên b
Tính diện tích toàn phần của :
a) Hình chóp tứ giác đều, biết cạnh đáy \(a=5cm\), cạnh bên \(b=5cm,\sqrt{18,75}\approx4,33\)
b) Hình chóp lục giác đều, biết cạnh đáy \(a=6cm\), cạnh bên \(b=10cm,\sqrt{3}\approx1,73,\sqrt{91}\approx9,54\)
Một hình chóp tứ giác đều là một lăng trụ đứng tứ giác đều như hình 147 dưới đây (cạnh đáy và chiều cao bằng nhau) :
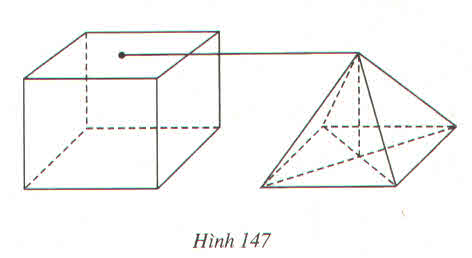
Nếu thể tích lăng trụ là V thì thể tích hình chóp là :
(A) \(V\) (B) \(\dfrac{V}{2}\)
(C) \(\dfrac{V}{3}\) (D) \(\dfrac{V}{4}\)
Hãy chọn kết quả đúng ?
