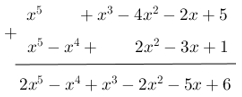Thu gọn rồi sắp xếp đa thức theo lũy thừa giảm của biến :
f(x)=x5−3x2+x3−x2−2x+5⇔f(x)=x5+x3−x2−2x+5f(x)=x5−3x2+x3−x2−2x+5⇔f(x)=x5+x3−x2−2x+5
g(x)=x2−3x+1+x2−x4+x5⇔g(x)=x5−x4+2x2−3x+1g(x)=x2−3x+1+x2−x4+x5⇔g(x)=x5−x4+2x2−3x+1
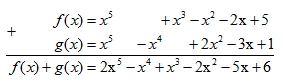
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):