Question

Tính đường chéo của 1 mặt bàn hình chữ nhật có chiều dài 120cm, chiều rộng 60cm

Answer 1

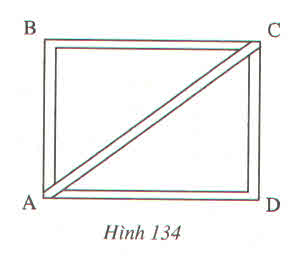
Gọi mặt bàn đó là hình chữ nhật ABC.

Theo định lí Py-ta-go, ta có:

AB² + BC² = AC²

Mà AB = (CD) = 120cm, BC = (AC) = 60

⇒ AC² = 120² + 60² ⇒ 14400 + 3600 = 18000

⇒ AC = \(\sqrt[]{18000}\)

Vậy đường chéo của mặt bàn hình chữ nhật đó là \(\sqrt[]{18000}\)cm.

Answer 2

Giả sử mặt bàn là hình chữ nhật \(ABCD\), chiều rộng là AD, chiều dài là AB, đường chéo là BD.

+ Xét \(\Delta ABD\) vuông tại \(A\) có:

\(BD^2=AB^2+AD^2\) (định lí Py - ta - go).

=> \(BD^2=120^2+60^2\)

=> \(BD^2=14400+3600\)

=> \(BD^2=18000\)

=> \(BD=\sqrt{18000}\)

=> \(BD=60\sqrt{5}\left(cm\right)\) (vì \(BD>0\)).

Vậy đường chéo của mặt bàn hình chữ nhật là: \(60\sqrt{5}\left(cm\right).\)

Chúc bạn học tốt!