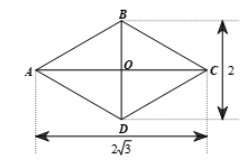
Theo đề bài ta có: \(AC = 2\sqrt3;\; BD = 2\).
Gọi giao điểm của hai đường chéo AC và BD là O.
Suy ra \(AO = OC = \sqrt3\); \(BO = OD = 1\).
Xét tam giác AOB vuông tại O, ta có:
\(tan ABO = \frac{AO}{BO}=\frac{\sqrt3}{1} =\sqrt3\)
Suy ra \(\widehat{ABO} = 60^\circ\) suy ra \(\widehat{BAO} = 90^\circ - 60^\circ = 30^\circ\)
Theo tính chất hình thoi, ta có:
\(\widehat{ABC} = 2\widehat{ABO} = 120^\circ\)
\(\widehat{BAD} = 2\widehat{BAO} = 60^\circ\)
Vậy hình thoi có các góc là \(120^\circ\) và \(60^\circ\).
Đúng 0
Bình luận (0)


