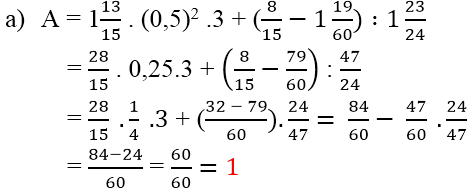a, \(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
= \(\dfrac{28}{15}.\dfrac{25}{100}.3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right):\dfrac{47}{24}\)
= \(\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{32-79}{60}\right).\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-47}{60}.\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-24}{60}=\dfrac{60}{60}=1\)
b, \(\dfrac{\left(\dfrac{11^2}{200}+0,415\right):0,01}{\dfrac{1}{12}-37,25+3\dfrac{1}{6}}\)
= \(\dfrac{\left(\dfrac{121}{200}+\dfrac{415}{1000}\right):\dfrac{1}{100}}{\dfrac{1}{12}-\dfrac{3725}{100}+\dfrac{19}{6}}=\dfrac{\left(\dfrac{121}{200}+\dfrac{83}{200}\right).100}{\dfrac{1}{12}-\dfrac{149}{4}+\dfrac{19}{6}}\)
= \(\dfrac{\dfrac{51}{50}.100}{-34}=\dfrac{102}{-34}=-3\)
a, 11315.(0,5)2.3+(815−11960):1232411315.(0,5)2.3+(815−11960):12324
= 2815.25100.3+(815−7960):47242815.25100.3+(815−7960):4724
= 2815.14.3+(32−7960).24472815.14.3+(32−7960).2447
= 8460+−4760.24478460+−4760.2447
= 8460+−2460=6060=18460+−2460=6060=1
b, (112200+0,415):0,01112−37,25+316(112200+0,415):0,01112−37,25+316
= (121200+4151000):1100112−3725100+196=(121200+83200).100112−1494+196(121200+4151000):1100112−3725100+196=(121200+83200).100112−1494+196
= 5150.100−34=102−34=−3
A=28/15.1/4.3+-47/60:47/24
=7/5+-2/5
=1