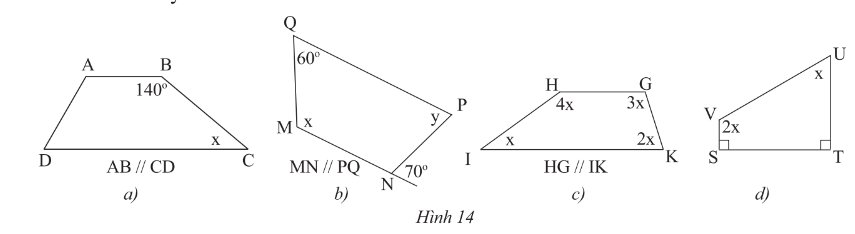
a) Vì \(AB\) // \(CD\) (gt) suy ra:
\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)
\(\begin{array}{l}140^\circ + x = 180^\circ \\x = 40^\circ \end{array}\)
b) Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)
\(\begin{array}{l}x + 60^\circ = 180^\circ \\x = 120^\circ \end{array}\)
Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat P = \widehat N = 70^\circ \) (so le trong)
c) Xét tứ giác \(IHGK\) ta có:
\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)
d) Xét tứ giác \(UVST\) ta có:
\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)
\(\begin{array}{l}x + 2x + 90^\circ + 90^\circ = 360^\circ \\3x + 180^\circ = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)