Ta có: \(-1\le cos\left(x\right)\le1\Rightarrow-2\le2cos\left(x\right)\le2\Rightarrow-1\le2cos\left(x\right)+1\le3\)
Vậy tập giá trị của hàm số là \(T\left[-1;3\right]\)
Ta có: \(-1\le cos\left(x\right)\le1\Rightarrow-2\le2cos\left(x\right)\le2\Rightarrow-1\le2cos\left(x\right)+1\le3\)
Vậy tập giá trị của hàm số là \(T\left[-1;3\right]\)
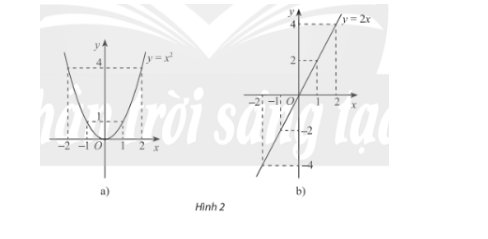
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
Dựa vào đồ thị của hàm số \(y = sinx\), xác định các giá trị \(x \in [ - \pi ;\pi ]\;\)thoả mãn \(sinx = \frac{1}{2}\)
Tìm tập xác định của các hàm số sau:
\(\begin{array}{l}a)\;y = \frac{1}{{cosx}}\\b)\;y = tan(x + \frac{\pi }{4})\\c)\;y = \frac{1}{{2 - si{n^2}x}}\end{array}\)
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác \(\alpha \; = \;(Ox,OM)\) theo hàm số \({v_x} = 0,3sin\alpha \;\) (m/s) (Hình 11).
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của \({v_x}\)
b) Dựa vào đồ thị của hàm số sin, hãy cho biết trong vòng quay đầu tiên \((0 \le \alpha \le 2\alpha )\), góc \(\alpha \)ở trong các khoảng nào thì \({v_x}\) tăng.
Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, \(\alpha \) là góc lượng giác \((Tx,{\rm{ }}TA)\) \((0 < \alpha < \pi ).\)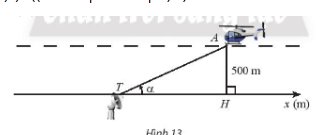
a) Biểu diễn toạ độ \({x_H}\) của điểm H trên trục \({T_x}\) theo \(\alpha \).
b) Dựa vào đồ thị hàm số côtang, hãy cho biết với \(\frac{\pi }{6} < \alpha < \frac{{2\pi }}{3}\) thì \({x_H}\) nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ
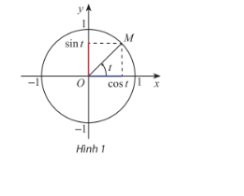
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác. Sử dụng định nghĩa của các giá trị lượng giác, hãy giải thích vì sao xác định duy nhất:
a) Giá trị sint và cost
b) Giá trị tant (nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)) và \(\cot t\)(nếu \(t \ne k\pi ,k \in \mathbb{Z}\)).
Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 1 giây đầu thì li độ s nằm trong đoạn \(\left[ { - 1;1} \right]\,\,(cm)\).
