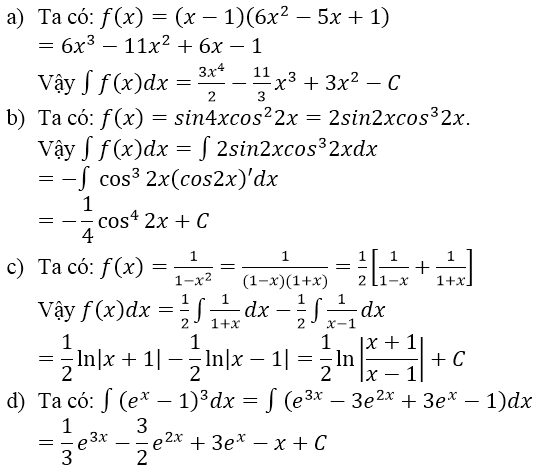Bài 4: Ôn tập chương nguyên hàm, tích phân và ứng dụng
Các câu hỏi tương tự
12 tháng 11 2021 lúc 20:34
Cho hàm số y = f(x) liên tục trên \(\left[0;2\right]\), thỏa mãn các điều kiện f(2) = 1 và \(\int\limits^2_0f\left(x\right)dx=\int\limits^2_0\left[f'\left(x\right)\right]^2dx=\dfrac{2}{3}\) Giá trị của f(1) bằng
12 tháng 11 2021 lúc 20:37
Cho hàm số f(x) có đạo hàm liên tục trên đoạn \(\left[0;1\right]\) thỏa mãn f(1) = 1 và (f'(x)2 + 4(6x2 -1).f(x) = 40x6 - 44x4 + 32x2 - 4, mọi x thuộc \(\left[0;1\right]\). Giá trị f(\(\dfrac{1}{2}\)) bằng ?
12 tháng 11 2021 lúc 22:26
Cho hàm số f(x) thỏa mãn f'(x) + 2x.f(x) = f(x).lnx với f(x)≠ 0, ∀x và f(1) =1. Khi đó \(\left|f\left(2\right)\right|\) bằng ?
12 tháng 11 2021 lúc 22:32
Cho hàm số f(x) thỏa mãn: xf'(x).lnx + f(x) = 2x2, ∀x ∈ (1;+∞) và f(e) = e2. Tính tích phân I=\(\int\limits^{e^2}_e\dfrac{x}{f\left(x\right)}dx\)
Tính :
a) intleft(2-xright)sin xdx
b) intdfrac{left(x+1right)^2}{sqrt{x}}dx
c) intdfrac{3^{3x}+1}{e^x+1}dx
d) intdfrac{1}{left(sin x+cos xright)^2}dx
e) intdfrac{1}{sqrt{1+x}+sqrt{x}}dx
g) intdfrac{1}{left(1+xright)left(2-xright)}dx
Đọc tiếp
Tính :
a) \(\int\left(2-x\right)\sin xdx\)
b) \(\int\dfrac{\left(x+1\right)^2}{\sqrt{x}}dx\)
c) \(\int\dfrac{3^{3x}+1}{e^x+1}dx\)
d) \(\int\dfrac{1}{\left(\sin x+\cos x\right)^2}dx\)
e) \(\int\dfrac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
g) \(\int\dfrac{1}{\left(1+x\right)\left(2-x\right)}dx\)
Tính :
a) intlimits^{dfrac{pi}{2}}_0cos2x.sin^2dx
b) intlimits^1_{-1}left|2^x-2^{-x}right|dx
c) intlimits^2_1dfrac{left(x+1right)left(x+2right)left(x+3right)}{x^2}dx
d) intlimits^2_0dfrac{1}{x^2-2x-3}dx
e) intlimits^{dfrac{pi}{2}}_0left(sin x+cos xright)^2dx
g) intlimits^{pi}_0left(x+sin xright)^2dx
Đọc tiếp
Tính :
a) \(\int\limits^{\dfrac{\pi}{2}}_0\cos2x.\sin^2dx\)
b) \(\int\limits^1_{-1}\left|2^x-2^{-x}\right|dx\)
c) \(\int\limits^2_1\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)}{x^2}dx\)
d) \(\int\limits^2_0\dfrac{1}{x^2-2x-3}dx\)
e) \(\int\limits^{\dfrac{\pi}{2}}_0\left(\sin x+\cos x\right)^2dx\)
g) \(\int\limits^{\pi}_0\left(x+\sin x\right)^2dx\)
Tính các tích phân sau :
a) \(\int\limits^{\dfrac{\pi}{4}}_0\cos2x.\cos^2xdx\)
b) \(\int\limits^1_{\dfrac{1}{2}}\dfrac{e^x}{e^{2x}-1}dx\)
c) \(\int\limits^1_0\dfrac{x+2}{x^2+2x+1}\ln\left(x+1\right)dx\)
d) \(\int\limits^{\dfrac{\pi}{4}}_0\dfrac{x\sin x+\left(x+1\right)\cos x}{x\sin x+\cos x}dx\)
4.Cho hàm số f(x) là hàm số chẵn và liên tục trên R thỏa mãn int_{-1}^1fleft(xright)dx2. Khi đó giá trị tích phân int_0^1fleft(xright)dx là : A.1 B.2 C.frac{1}{4} D.frac{1}{2}
5.Cho f(x) liên tục trên [0;10] thỏa mãn int_0^{10}fleft(xright)dx7, int_2^6fleft(xright)dx3. Khi đó giá trị của P int_0^2fleft(xright)dx+int_6^{10}fleft(xright)dx có giá trị là: A.1 B.2 C.4 D.3
6.Cho hình phẳng S giới hạn bởi Ox và y sqrt{1-x^2}. Thể tích của khối tròn xoay khi quay S quanh Ox là: A.frac{3}...
Đọc tiếp
4.Cho hàm số f(x) là hàm số chẵn và liên tục trên R thỏa mãn \(\int_{-1}^1f\left(x\right)dx\)=2. Khi đó giá trị tích phân \(\int_0^1f\left(x\right)dx\) là : A.1 B.2 C.\(\frac{1}{4}\) D.\(\frac{1}{2}\)
5.Cho f(x) liên tục trên [0;10] thỏa mãn \(\int_0^{10}f\left(x\right)dx=7\), \(\int_2^6f\left(x\right)dx=3\). Khi đó giá trị của P = \(\int_0^2f\left(x\right)dx+\int_6^{10}f\left(x\right)dx\) có giá trị là: A.1 B.2 C.4 D.3
6.Cho hình phẳng S giới hạn bởi Ox và y =\(\sqrt{1-x^2}\). Thể tích của khối tròn xoay khi quay S quanh Ox là: A.\(\frac{3}{2}\pi\) B.\(\frac{3}{4}\pi\) C.\(\frac{4}{3}\pi\) D.\(\frac{2}{3}\pi\)
7.Tính tích phân I = \(\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\frac{\sin^2x}{\sin3x}dx\) ta được kết quả I = \(\frac{1}{a}ln\left|b+\sqrt{3c}\right|\) với a, b, c \(\in Z\). Giá trị của a + 2b + 3c là: A.5 B.2 C.8 D.3
8.Cho hàm số y = f(x) có đạo hàm f'(x) = \(\frac{1}{2x-1}\), f(1)=1 thì f(5) có giá trị bằng: A.ln2 B.ln2 + 1 C.ln3 D.ln3 + 1
Tính các tích phân sau :
a) intlimits^1_0left(y-1right)^2sqrt{y}dy, đặt tsqrt{y}
b) intlimits^2_1left(x^2+1right)sqrt[3]{left(z-1right)^2}dz, đặt usqrt[3]{z-1}
c) intlimits^e_1dfrac{sqrt{4+5ln x}}{x}dx
d) intlimits^{dfrac{pi}{2}}_0left(cos^5varphi-sin^5varphiright)dvarphi
e) intlimits^{pi}_0cos^3alphacos3alpha dalpha
Đọc tiếp
Tính các tích phân sau :
a) \(\int\limits^1_0\left(y-1\right)^2\sqrt{y}dy\), đặt \(t=\sqrt{y}\)
b) \(\int\limits^2_1\left(x^2+1\right)\sqrt[3]{\left(z-1\right)^2}dz\), đặt \(u=\sqrt[3]{z-1}\)
c) \(\int\limits^e_1\dfrac{\sqrt{4+5\ln x}}{x}dx\)
d) \(\int\limits^{\dfrac{\pi}{2}}_0\left(\cos^5\varphi-\sin^5\varphi\right)d\varphi\)
e) \(\int\limits^{\pi}_0\cos^3\alpha\cos3\alpha d\alpha\)