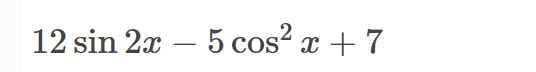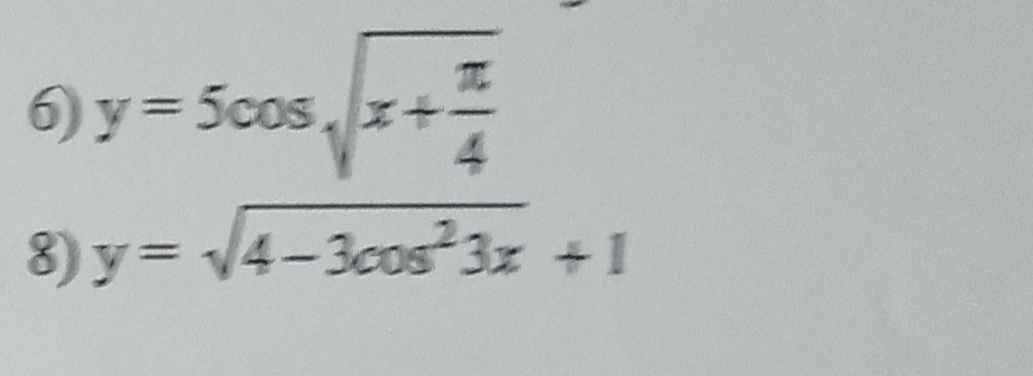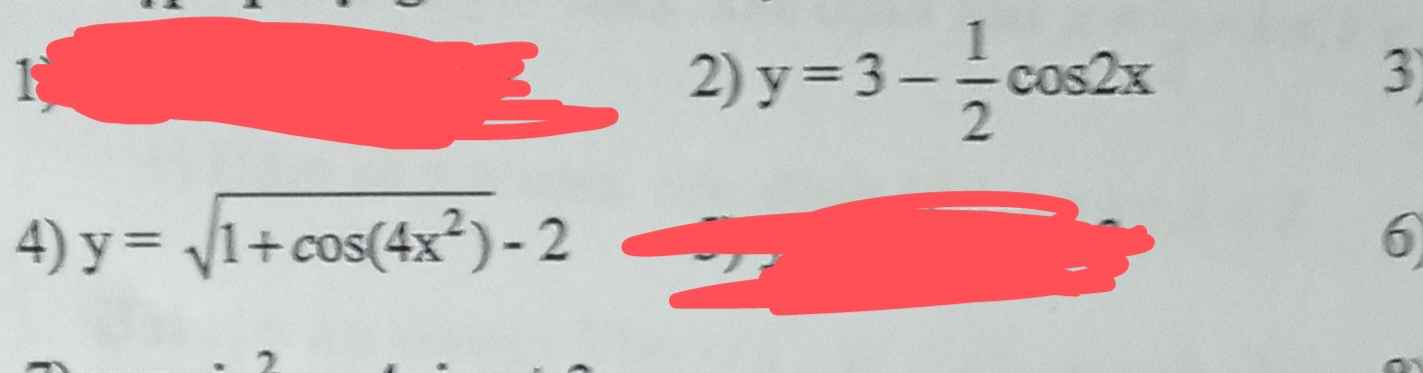\(y=-5\cdot\dfrac{1-cos2x}{2}+12sin2x+7\)
\(=-\dfrac{5}{2}+\dfrac{5}{2}\cdot cos2x+12\cdot sin2x+7\)
\(=12\cdot sin2x+\dfrac{5}{2}\cdot cos2x+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(\dfrac{12\cdot sin2x}{\dfrac{\sqrt{601}}{2}}+cos2x\cdot\dfrac{5}{2}\cdot\dfrac{2}{\sqrt{601}}\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(sin2x\cdot cosa+cos2x\cdot sina\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)+\dfrac{9}{2}\)
\(-1< =sin\left(2x+a\right)< =1\)
=>\(\dfrac{-\sqrt{601}}{2}< =\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)< =\dfrac{\sqrt{601}}{2}\)
=>\(\dfrac{-\sqrt{601}+9}{2}< =y< =\dfrac{\sqrt{601}+9}{2}\)
\(y_{min}\) khi sin(2x+a)=-1
=>\(2x+a=-\dfrac{pi}{2}+k2pi\)
=>\(2x=-\dfrac{pi}{2}-a+k2pi\)
=>\(x=-\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)
\(y_{max}\) khi sin(2x+a)=1
=>\(2x+a=\dfrac{pi}{2}+k2pi\)
=>\(x=\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)