Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường.
a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.
b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.
Gọi A là biến cố: “Linh kiện điện tử đạt tiêu chuẩn”, B là biến cố: “linh kiện được đóng dấu OTK”.
Ta có: \(P\left( A \right) = 0,8 \Rightarrow P\left( {\overline A } \right) = 0,2\), \(P\left( {B|A} \right) = 0,99,P\left( {\overline B |\overline A } \right) = 0,95\)
Ta có: \(P\left( {B|\overline A } \right) = 1 - 0,95 = 0,05\)
a) Xác suất để linh kiện được đóng dấu OTK là:
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,8.0,99 + 0,2.0,05 = 0,802\)
b) Ta có sơ đồ hình cây:
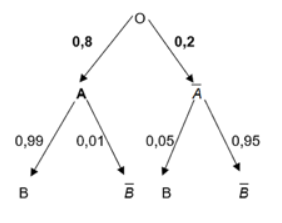
Trên nhánh OA và \(O\overline A \) tương ứng ghi P(A) và \(P\left( {\overline A } \right)\);
Trên nhánh AB và \(A\overline B \) tương ứng ghi \(P\left( {B|A} \right)\) và \(P\left( {\overline B |A} \right)\);
Trên nhánh \(\overline A B\) và \(\overline {AB} \) tương ứng ghi \(P\left( {B|\overline A } \right)\) và \(P\left( {\overline B |\overline A } \right)\).
Có hai nhánh cây đi tới \(\overline B \) là \[OA\overline B \] và \(O\overline A \overline B \)
Do đó, \(P\left( {\overline B } \right) = 0,8.0,01 + 0,95.0,2 = 0,198\)
Vậy xác suất để linh kiện điện tử được chọn không được đóng dấu OTK là 0,198.


