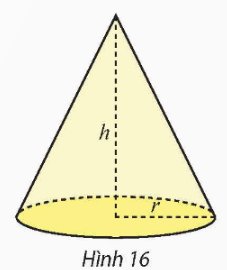
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)