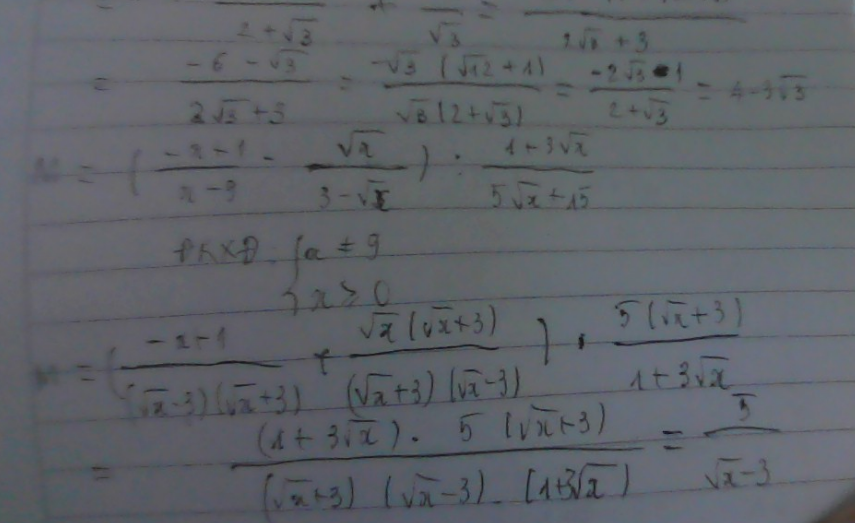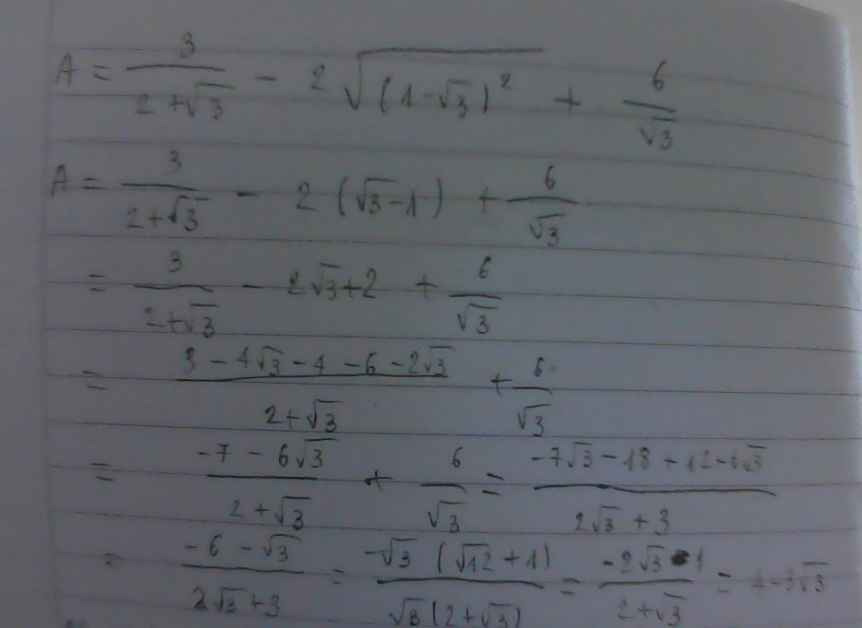Question

Rút gọn biểu thức

A= \(\dfrac{3}{2+\sqrt{3}}-2\sqrt{\left(1-\sqrt{3}\right)^2}+\dfrac{6}{\sqrt{3}}\)

M=\(\left(\dfrac{-x+1}{x-9}-\dfrac{\sqrt{x}}{3-\sqrt{x}}\right):\dfrac{1+3\sqrt{x}}{5\sqrt{x}+15}\)

Answer 1

Answer 2

\(A=\dfrac{3}{2+\sqrt{3}}-2\sqrt{\left(1-\sqrt{3}\right)^2}+\dfrac{6}{\sqrt{3}}\\ =\dfrac{3\left(2-\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}-2\left|1-\sqrt{3}\right|+\dfrac{6\sqrt{3}}{3}\\ =3\left(2-\sqrt{3}\right)-2\left(\sqrt{3}-1\right)+2\sqrt{3}\\ =6-3\sqrt{3}-2\sqrt{3}+2+2\sqrt{3}\\ =8-3\sqrt{3}\)

 

\(M=\left(\dfrac{-x+1}{x-9}-\dfrac{\sqrt{x}}{3-\sqrt{x}}\right):\dfrac{1+3\sqrt{x}}{5\sqrt{x}+15}\\ =\left(\dfrac{-x+1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\dfrac{1+3\sqrt{x}}{5\left(\sqrt{x}+3\right)}\\ =\dfrac{-x+1+x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{1+3\sqrt{x}}{5\left(\sqrt{x}+3\right)}\\ =\dfrac{1+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{1+3\sqrt{x}}{5\left(\sqrt{x}+3\right)}\\ =\dfrac{5}{\sqrt{x}-3}\)