a) Chia cả tử và mẫu của phân số \(\frac{{ - 20}}{{30}}\) cho -5 thì được phân số \(\frac{4}{{ - 6}}\)
b) Hai phân số này bằng nhau, vì \[ - 20.( - 6) = {\rm{ }}4.30\]
c) Ví dụ: Phân số \(\frac{{ - 9}}{{12}}\) và phân số \(\frac{{ - 3}}{4}\)
a) Chia cả tử và mẫu của phân số \(\frac{{ - 20}}{{30}}\) cho -5 thì được phân số \(\frac{4}{{ - 6}}\)
b) Hai phân số này bằng nhau, vì \[ - 20.( - 6) = {\rm{ }}4.30\]
c) Ví dụ: Phân số \(\frac{{ - 9}}{{12}}\) và phân số \(\frac{{ - 3}}{4}\)
Quan sát hai phân số \(\frac{3}{{ - 5}}\) và \(\frac{{ - 21}}{{35}}\) và cho biết:
a) Nhân cả tử và mẫu của phân số với cùng số nguyên nào thì được phân số \(\frac{{ - 21}}{{35}}\)
b) Hai phân số đó có bằng nhau không?
c) Nêu ví dụ tương tự.
Viết mỗi phân số dưới đây thành phân số bằng nó có mẫu số dương:
\(\frac{1}{{ - 2}}\); \(\frac{{ - 3}}{{ - 5}}\); \(\frac{2}{{ - 7}}\).
Áp dụng tính chất 1 và tính chất 2 để tìm một phân số bằng mỗi phân số sau:
a) \(\frac{{21}}{{13}}\); b) \(\frac{{12}}{{ - 25}}\); c) \(\frac{{18}}{{ - 48}}\); d) \(\frac{{ - 42}}{{ - 24}}\).
Viết phân số \(\frac{3}{{ - 5}}\) thành phân số có mẫu dương.
Rút gọn các phân số sau:
\(\frac{{12}}{{ - 24}}\); \(\frac{{ - 39}}{{75}}\); \(\frac{{132}}{{ - 264}}\).
Rút gọn các phân số \(\frac{{ - 18}}{{76}}\); \(\frac{{125}}{{ - 375}}\).
Dùng phân số có mẫu số dương nhỏ nhất để biểu thị xem số phút sau đây chiếm bao nhiêu phần của một giờ?
a) 15 phút; b) 20 phút; c) 45 phút; d) 50 phút.
Dùng phân số để viết mỗi khối lượng sau theo tạ, theo tấn.
a) 20 kg; b) 55 kg; c) 87 kg d) 91 kg.
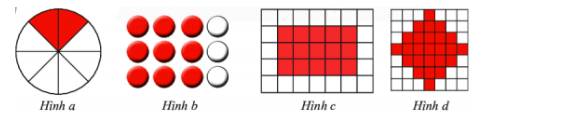
Dùng phân số có mẫu số dương nhỏ nhất biểu thị phần tô màu trong mỗi hình sau.