Question

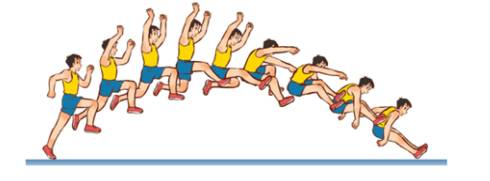
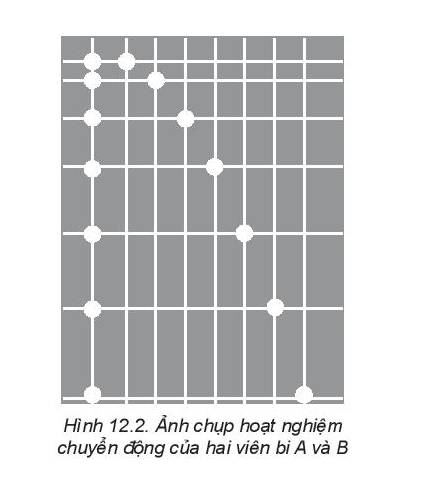
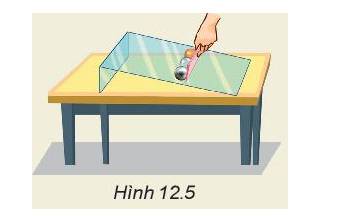
Người ta bắn một viên bi với vận tốc ban đầu 4 m/s theo phương xiên 450 so với phương nằm ngang. Coi sức cản của không khí là không đáng kể.

1. Tính vận tốc của viên bi theo phương nằm ngang và phương thẳng đứng tại các thời điểm: bắt đầu bắn, sau 0,1 s và sau 0,2 s.

2.

a) Viên bi đạt tầm cao H vào lúc nào?

b) Tính tầm cao H.

c) Gia tốc của viên bi ở tầm cao H có giá trị bằng bao nhiêu?

3.

a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí nào?

b) Viên bi có vận tốc cực tiểu vào thời điểm nào?

4.

a) Khi nào thì viên bi chạm sàn?

b) Xác định vận tốc của viên bi khi chạm sàn.

c) Xác định tầm xa L của viên bi.

Answer 1

 

1.

+ Vận tốc ban đầu của viên bi theo phương ngang: \({v_{0x}} = {v_0}.\cos \alpha  = 4.\cos {45^0} = 2\sqrt 2 (m/s)\)

+ Vận tốc ban đầu của viên bi theo phương thẳng đứng: \({v_{0y}} = {v_0}.\sin \alpha  = 4.\sin {45^0} = 2\sqrt 2 (m/s)\)

+ Vận tốc của viên bi theo phương ngang sau 0,1 s và sau 0, 2 s là \({v_{0x}} = 2\sqrt 2 m/s\)

+ Vận tốc của viên bi theo phương thẳng đứng sau 0,1 s là: \({v_y} = {v_{0y}} - gt = 2\sqrt 2  - 9,8.0,1 \approx 1,85(m/s)\)

+ Vận tốc của viên bi theo phương thẳng đứng sau 0,2 s là:

\({v_y} = {v_{0y}} - gt = 2\sqrt 2  - 9,8.0,2 \approx 0,87(m/s)\)

Answer 2

2.

a) Thời gian viên bi đạt tầm cao H: \(t = \frac{{{v_{0y}}}}{g} = \frac{{2\sqrt 2 }}{{9,8}} \approx 0,29(s)\)

b) Tầm cao H là: \(H = \frac{{v_{0y}^2}}{{2.g}} = \frac{{{{(2\sqrt 2 )}^2}}}{{2.9,8}} \approx 0,4(m)\)

c) Gia tốc của viên bi ở tầm cao H là: a = g = 9,8 (m/s² )

Answer 3

3.

a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao H = 0,4 m

b) Viên vi có vận tốc cực tiểu vào thời gian: t = 0,29 s

Answer 4

4.

a) Thời gian viên bi chạm mặt sàn là: \(t = \frac{{2.{v_{0y}}}}{g} = \frac{{2.2\sqrt 2 }}{{9,8}} \approx 0,58(s)\)

b) Vận tốc của viên bi khi chạm đất là:

\(\begin{array}{l}v_y^2 = v_{0y}^2 + 2gh\\ \Rightarrow {v_y} = \sqrt {v_{0y}^2 + 2gh}  = \sqrt {{{(2\sqrt 2 )}^2} + 2.9,8.0,4}  \approx 4(m/s)\end{array}\)

c) Tầm xa của viên bi là:

\(L = \frac{{v_0^2.{{\sin }^2}2\alpha }}{g} = \frac{{{{(2\sqrt 2 )}^2}.{{\sin }^2}{{90}^0}}}{{9,8}} \approx 0,82(m)\)