Độ dài đường chéo hình hộp chữ nhật là: \(\sqrt{3^2+4^2+5^2}=5\sqrt{2}\)
\(\Rightarrow A\)
Độ dài đường chéo hình hộp chữ nhật là: \(\sqrt{3^2+4^2+5^2}=5\sqrt{2}\)
\(\Rightarrow A\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(b\), \(SA\) vuông góc với mặt đáy, \(SC = 2b\sqrt 2 \). Số đo góc giữa cạnh bên \(SC\) và mặt đáy là
A. \({60^ \circ }\).
B. \({30^ \circ }\).
C. \({45^ \circ }\).
D. \({50^ \circ }\).
Cho hình hộp \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = a\), đáy \(ABCD\) là hình thoi có \(AB = BD = a\). Hình chiếu vuông góc của \(A'\) lên mặt đáy trùng với điểm \(O\) là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
A. \({75^ \circ }46'\).
B. \({71^ \circ }21'\).
C. \({68^ \circ }31'\).
D. \({65^ \circ }12'\).
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng \(a\) là
A. \(\frac{{{a^3}\sqrt 3 }}{4}\).
B. \(\frac{{{a^3}\sqrt 3 }}{3}\).
C. \(\frac{{{a^3}\sqrt 2 }}{3}\).
D. \(\frac{{{a^3}\sqrt 2 }}{2}\).
Cho hình chóp tam giác đều \(S.ABC\) cạnh đáy bằng \(2a\) và chiều cao bằng \(a\sqrt 2 \). Khoảng cách từ tâm \(O\) của đáy \(ABC\) đến một mặt bên là
A. \(\frac{{a\sqrt {14} }}{7}\).
B. \(\frac{{a\sqrt 2 }}{7}\).
C. \(\frac{{a\sqrt {14} }}{2}\).
D. \(\frac{{2a\sqrt {14} }}{7}\).
Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ bằng \(a\) và chiều cao bằng \(\frac{{a\sqrt 6 }}{3}\) là
A. \(\frac{{7\sqrt 2 }}{8}{a^3}\).
B. \(\frac{{\sqrt 2 }}{4}{a^3}\).
C. \(\frac{{7\sqrt 2 }}{{12}}{a^3}\).
D. \(\frac{{7\sqrt 3 }}{4}{a^3}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt đáy. Đường thẳng \(C{\rm{D}}\) vuông góc với mặt phẳng nào sau đây?
A. \(\left( {SAD} \right)\).
B. \(\left( {SAC} \right)\).
C. \(\left( {SAB} \right)\).
D. \(\left( {SBD} \right)\).
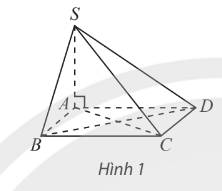
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); \(AB = AD = 2a;CD = a\); số đo góc nhị diện \(\left[ {S,BC,A} \right]\) bằng \({60^ \circ }\). Gọi \(I\) là trung điểm của cạnh \(A{\rm{D}}\). Biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Tính thể tích khối chóp \(S.ABCD\) theo \(a\).
Cho hình chóp \(S.ABCD\) có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(M\) là trung điểm của \({\rm{S}}A\). Mặt phẳng \(\left( {MBD} \right)\) vuông góc với mặt phẳng nào dưới đây?
A. \(\left( {SBC} \right)\).
C. \(\left( {SBD} \right)\).
B. \(\left( {SAC} \right)\).
D. \(\left( {ABCD} \right)\).