Vì G là trọng tâm của △PQR nên theo tính chất trọng tâm ta có :
\(PG=\frac{2}{3}PX\)
⇒ \(GX=\frac{1}{3}PX\)
⇒ \(\frac{PG}{GX}=\frac{2}{3}PX:\frac{1}{3}PX=2\)
Vậy tỷ số \(\frac{PG}{GX}\) bằng 2:1
Bài 4: Tính chất ba đường trung tuyến của tam giác
Các câu hỏi tương tự
Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng :
a) Các cạnh của tam giác BGD bằng \(\dfrac{2}{3}\) các đường trung tuyến của tam giác ABC
b) Các đường trung tuyến của tam giác BGD bằng một nửa các cạnh của tam giác ABC
Cho tam giác ABC cân tai A có AH là đường trung tuyến ứng với cạnh BC A)chứng minh tâm giác AHB=tam giác AHC B)kẻ các đường trung tuyến BM và CN .Gọi G là trọng tâm của tam giác ABC Chứng minh tam giác GBC là tam giác cân C)qua C kẻ đường thẳng vuông góc với BC cắt đường thẳng BM tại từ G kẻ đường thẳng song song với BC. Chứng minh BC=2×GD
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
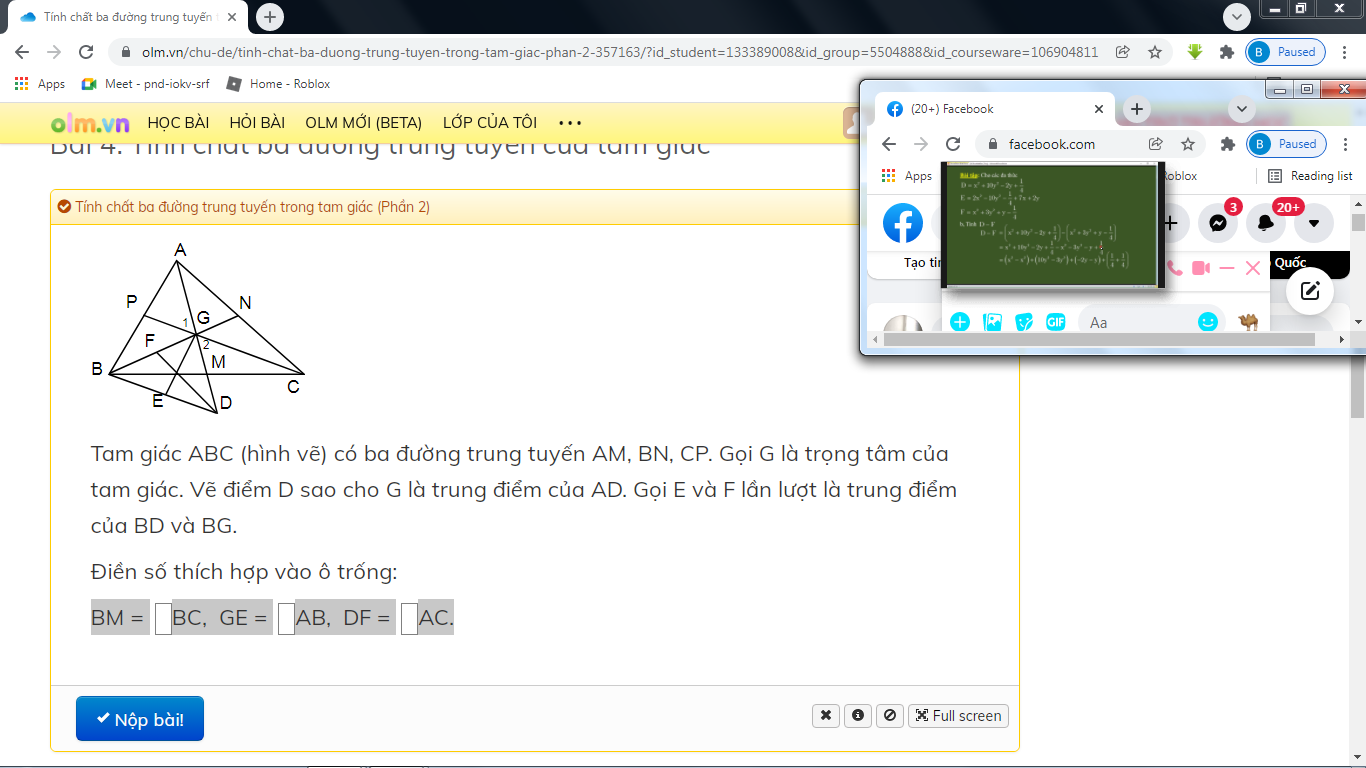
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BM =....BC, GE =.....AB, DF =........AC
Bài 1: Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H. Gọi D làtrung điểm của cạnh AC, E là giao điểm của AH và BD. Chứng minh rằng E làtrọng tâm của tam giác ABC.Bài 2: Cho tam giác ABC, AM là đường trung tuyến và G là trọng tâm. Đườngthẳng m qua M (m khác BC và AM). Vẽ BD vuông góc với m tại D, CE vuông gócvới m tại E. Chứng minh rằng G là trọng tâm của tam giác ADE.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H. Gọi D là
trung điểm của cạnh AC, E là giao điểm của AH và BD. Chứng minh rằng E là
trọng tâm của tam giác ABC.
Bài 2: Cho tam giác ABC, AM là đường trung tuyến và G là trọng tâm. Đường
thẳng m qua M (m khác BC và AM). Vẽ BD vuông góc với m tại D, CE vuông góc
với m tại E. Chứng minh rằng G là trọng tâm của tam giác ADE.
Cho tam giác ABC.Vẽ trung tuyến BM.Trên tía BM lấy G và K sao cho BG=2/3BM và G là trung điểm của BK.Gọi N là trung điểm của KC,GN cắt CM ở O .Chứng minh
a)O là trọng tâm tam giác GKC
b)GO=1/3 BC
giải hộ mình với
Tam giác ABC đều cạnh là 8cm. G là trọng tâm của tam giác ABC, trung tuyến AD, BE, CF.
a/ Tính AD, CG
b/ Chứng minh GA = GB + GC
Tam giác ABC có đường trung tuyến là AM,G là trọng tâm, biết AG bằng 4cm tính AM
cho tam giác ABC có đường trung tuyến AM.gọi G là trọng tâm của tam giác ABC.Qua C dựng đường thẳng song song BG cắt AM tại N .cmr a,tam giác BGM=tam giác CNM b,GA=Gn