Pha dao động của phương trình là: `10 \pi t + \varphi/2`
`=>` Pha dao động tại thời điểm `1/30 s` là: `10\pi .1/30 + \varphi/2=\pi/3+ \varphi/2`.
Pha dao động của phương trình là: `10 \pi t + \varphi/2`
`=>` Pha dao động tại thời điểm `1/30 s` là: `10\pi .1/30 + \varphi/2=\pi/3+ \varphi/2`.
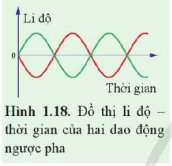
Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha.
Dựa vào đồ thị, xác định độ lệch pha của hai dao động này.
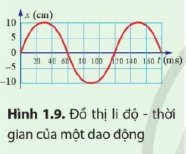
Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ thời gian được biểu diễn ở Hình 1.9.
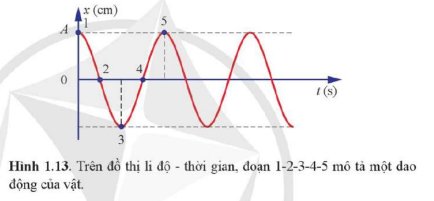
Xác định pha của dao động tại vị trí 3 và vị trí 4.
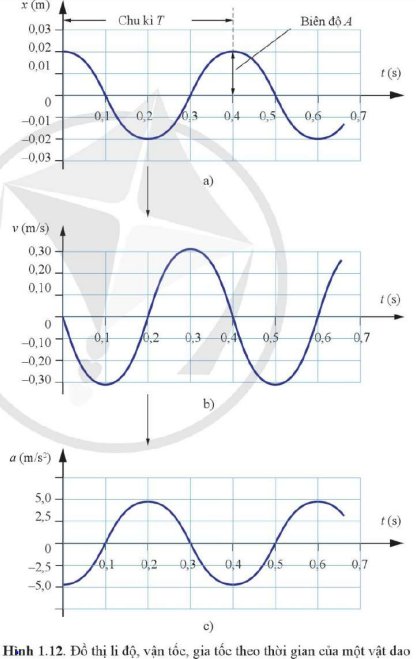
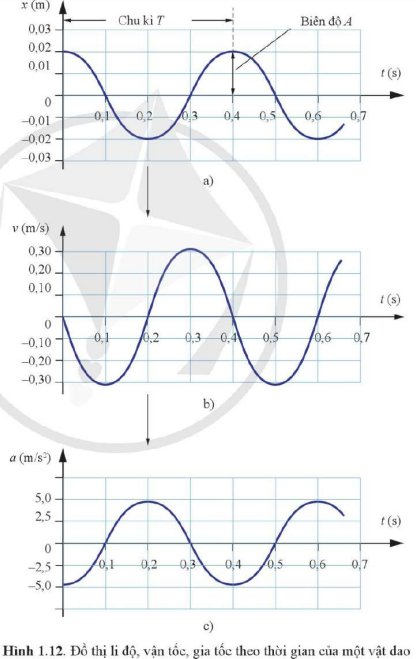
Dựa vào đồ thị Hình 1.12, xác định các đại lượng sau:
a) Tần số góc của dao động.
b) Biên độ của dao động.
c) Vận tốc cực đại của vật dao động.
d) Gia tốc cực đại của vật dao động.
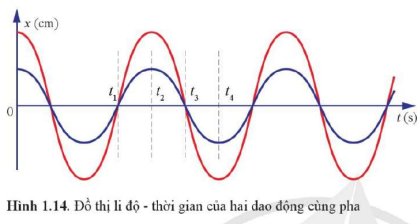
Mô tả trạng thái của hai vật dao động ở thời điểm t3 và t4 trong đồ thị Hình 1.14.
Thế nào là dao động điều hòa?
Tần số góc và tần số của dao động điều hòa có liên hệ như thế nào?
Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm.
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).
Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …
Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.