Question

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

Answer 1

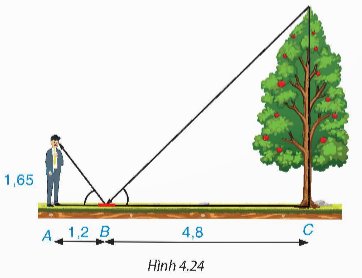
Gọi D là điểm tại mắt của người đứng, E là điểm trên đầu ngọn cây, ta có hình vẽ sau;

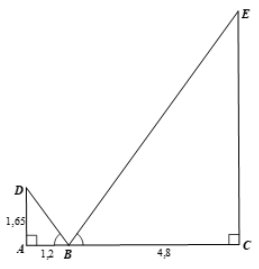
Chiều cao của cây là đoạn EC

Ta có \(\tan \widehat {ABD} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}\) hay \(\tan \widehat {EBC} = \frac{{11}}{8}\) (do \(\widehat {ABC} = \widehat {DBC}\))

Mà \(\tan \widehat {EBC} = \frac{{EC}}{{BC}}\) suy ra \(\frac{{EC}}{{4,8}} = \frac{{11}}{8}\) hay \(EC = \frac{{11}}{8}.4,8 = 6,6\) m

Vậy chiều cao của cây là 6,6 m.