Một chiếc máy quay phim ở đài truyền hình được đặt trên một giá đỡ ba chân với điểm đặt P(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là Q1(0; – 1; 0), Q2\(\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2};0\right)\), Q3\(\left(-\dfrac{\sqrt{3}}{2};\dfrac{1}{2};0\right)\) (Hình 35). Biết rằng trọng lượng của máy quay là 360 N.
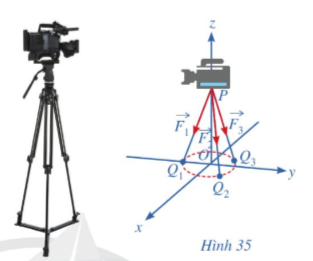
Làm thế nào để tìm được tọa độ của các lực \(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\) tác dụng lên giá đỡ?
Theo giả thiết, ta có các điểm P(0; 0; 4), \(Q_1\left(0;-1;0\right),Q_2\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2};0\right),Q_3\left(-\dfrac{\sqrt{3}}{2};\dfrac{1}{2};0\right)\)
\(\Rightarrow\overrightarrow{PQ1}=\left(0-0;-1-0;0-4\right)\) hay \(\overrightarrow{PQ_1}=\left(0;-1;-4\right);\)
\(\overrightarrow{PQ_2}=\left(\dfrac{\sqrt{3}}{2}-0;\dfrac{1}{2}-0;0-4\right)\) hay \(\overrightarrow{PQ_2}=\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2};-4\right);\)
\(\overrightarrow{PQ_3}=\left(-\dfrac{\sqrt{3}}{2}-0;\dfrac{1}{2}-0;0-4\right)\) hay \(\overrightarrow{PQ_3}=\left(-\dfrac{\sqrt{3}}{2};\dfrac{1}{2};-4\right)\)
\(\Rightarrow\left|\overrightarrow{PQ_1}\right|=\left|\overrightarrow{PQ_2}\right|=\left|\overrightarrow{PQ_3}\right|=\sqrt{17}\). Do đó \(\left|\overrightarrow{F_1}\right|=\left|\overrightarrow{F_2}\right|=\left|\overrightarrow{F_3}\right|\)
Vì vậy tồn tại hằng số c khác 0 sao cho:
\(\overrightarrow{F_1}=c\overrightarrow{PQ_1}=\left(0;-c;-4c\right);\\ \overrightarrow{F_2}=c\overrightarrow{PQ_2}=\left(\dfrac{\sqrt{3}}{2}c;\dfrac{1}{2}c;-4c\right);\\ \overrightarrow{F_3}=c\overrightarrow{PQ_3}=\left(-\dfrac{\sqrt{3}}{2}c;\dfrac{1}{2}c;-4c\right)\)
\(\Rightarrow\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;-12c\right).\)
Mặt khác ta có \(\overrightarrow{F_1}=\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{F}\) trong đó \(\overrightarrow{F}=\left(0;0;-360\right)\) là trọng lực tác dụng lên máy quay. => -12c = -360 => c = 30
Vậy\(\overrightarrow{F_1}=\left(0;-30;-120\right);\overrightarrow{F_2}=\left(15\sqrt{3};15;-120\right);\overrightarrow{F_3}=\left(-15\sqrt{3};15;-120\right).\)


