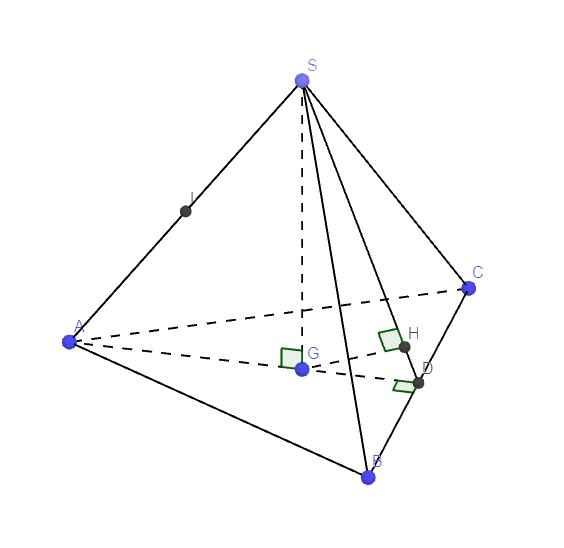
Do chóp SABC đều \(\Rightarrow SG\perp\left(ABC\right)\)
a. Gọi D là trung điểm BC \(\Rightarrow A,G,D\) thẳng hàng và \(AD\perp BC\)
\(\Rightarrow BC\perp\left(SAD\right)\) \(\Rightarrow\left(SBC\right)\perp\left(SAD\right)\)
Từ G kẻ \(GH\perp SD\Rightarrow GH\perp\left(SBC\right)\) do SD là giao tuyến 2 mp vuông góc (SBC) và (SAD)
\(\Rightarrow GH=d\left(G;\left(SBC\right)\right)\)
\(AD=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AD=\dfrac{a\sqrt{3}}{3}\\GD=\dfrac{1}{3}AD=\dfrac{a\sqrt{3}}{6}\end{matrix}\right.\)
\(SG=\sqrt{SA^2-AG^2}=\dfrac{a\sqrt{33}}{3}\)
Hệ thức lượng tam giác vuông SGD:
\(GH=\dfrac{SG.GD}{\sqrt{SG^2+GD^2}}=\dfrac{a\sqrt{165}}{45}\)
b.
Ta có: \(\left\{{}\begin{matrix}AG\cap\left(SBC\right)=D\\AD=3GD\end{matrix}\right.\)
\(\Rightarrow d\left(A;\left(SBC\right)\right)=3d\left(G;\left(SBC\right)\right)=\dfrac{a\sqrt{165}}{15}\)
c.
\(\left\{{}\begin{matrix}AI\cap\left(SBC\right)=S\\IS=\dfrac{1}{2}AS\end{matrix}\right.\) \(\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}d\left(A;\left(SBC\right)\right)=\dfrac{a\sqrt{165}}{30}\)
d.
Do K là trọng tâm tam giác SBC \(\Rightarrow K\in\left(SBC\right)\)
\(\Rightarrow d\left(K;\left(SBC\right)\right)=0\)
(Chắc câu này đề nhầm, K là trọng tâm SAC hay SAB thì hợp lý hơn)