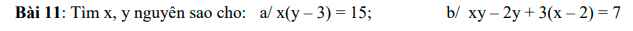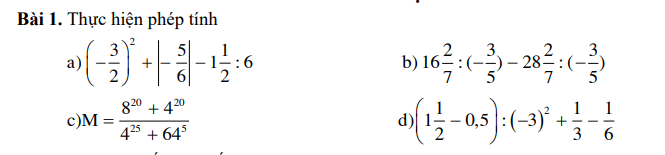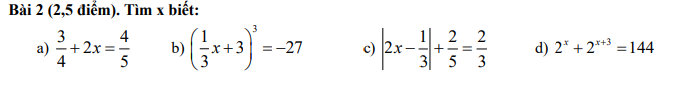4b)\(x^2-2y^2=1\)
\(\Rightarrow2y^2=x^2-1\) (1)
\(\Rightarrow2y^2=\left(x-1\right)\left(x+1\right)\)
Ta có:\(2y^2⋮2\Rightarrow\left(x-1\right)\left(x+1\right)⋮2\)\(\Rightarrow\)x lẻ\(\Rightarrow\left\{\begin{matrix}x-1⋮2\\x+1⋮2\end{matrix}\right.\Rightarrow\left(x-1\right)\left(x+1\right)⋮4\)
\(\Rightarrow2y^2⋮4\Rightarrow y^2⋮2\Rightarrow y⋮2\). Mà y nguyên tố nên y=2
Thay y =2 vào (1) ta được:
\(2.2^2=x^2-1\)
\(\Rightarrow x^2-1=8\)
\(\Rightarrow x^2=9\)
\(\Rightarrow x=3\)
Vậy x=3, y=2

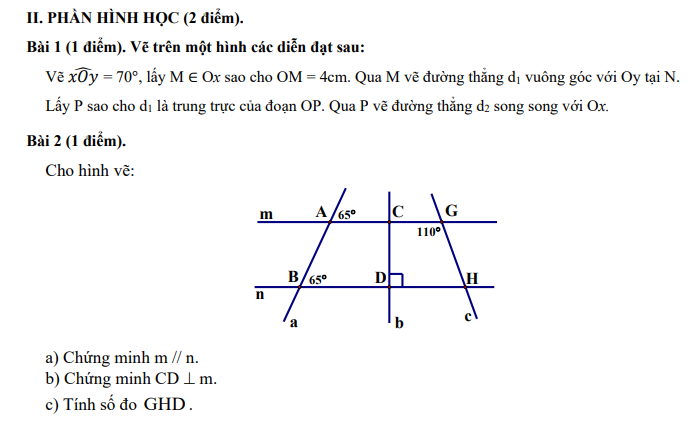
 Mọi người ơi, giúp tớ câu 2 và câu 4 nhé! Cảm ơn mọi người nhiều ạ!!!
Mọi người ơi, giúp tớ câu 2 và câu 4 nhé! Cảm ơn mọi người nhiều ạ!!!





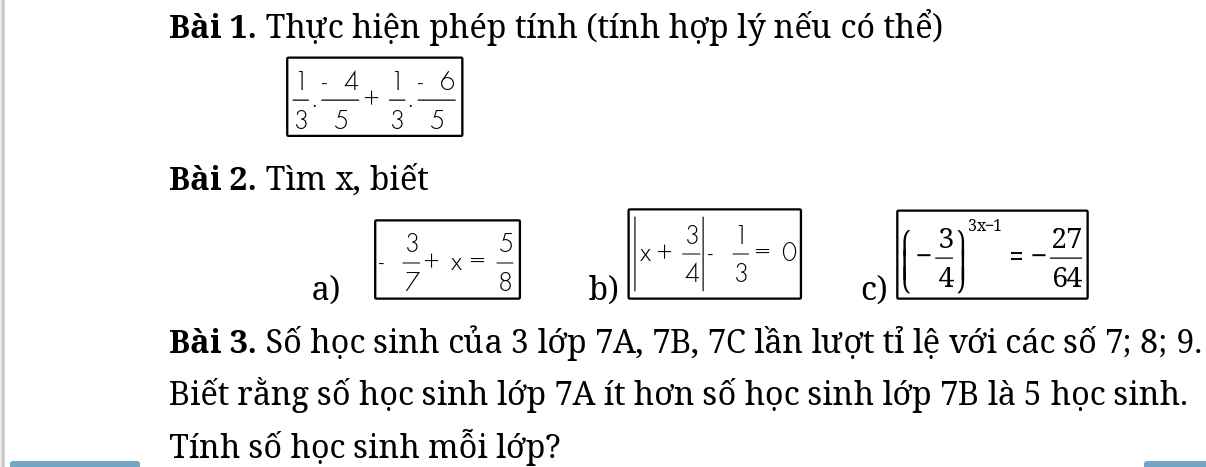 Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn
Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn