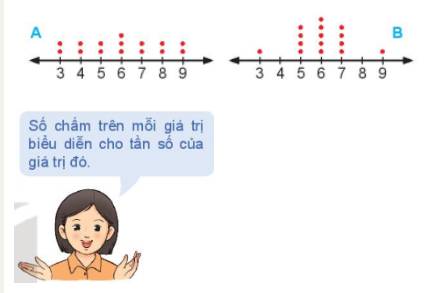
Mỗi khẳng định sau đúng hay sai?
(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.
(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại.
(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.
(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.
(5) Các số đo độ phân tán đều không âm.
Khẳng định (1): Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị so với giá trị trung bình càng nhỏ (tức là \({x_i} - \overline x \) càng nhỏ, với \(i = 1;2;...;n\)), dẫn đến độ lệch chuẩn càng nhỏ.
\(\Rightarrow\)(1) Sai
Khẳng định (2): Khoảng biến thiên R bằng hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất nên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất
\(\Rightarrow\) (2) Đúng.
Khẳng định (3): Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\), các giá trị \({Q_1},{Q_3}\) không bị ảnh hưởng bởi giá trị của giá trị lớn nhất và giá trị nhỏ nhất (với n>4)
\(\Rightarrow\) Sai
Khẳng định (4): Khoảng tứ phân vị chính là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp
\(\Rightarrow\) Sai.
Khẳng định (5): Các số đo độ phân tán là
Khoảng biến thiên R=Số lớn nhất – Số nhỏ nhất > 0
Trước khi tính khoảng tứ phân vị thì mẫu số liệu được sắp xếp theo thứ tự không giảm
\(\Rightarrow\) \({Q_3} > {Q_1}\) => \({\Delta _Q} = {Q_3} - {Q_1} > 0\)
Phương sai \({s^2} = \frac{{{{\left( {{x_1} - \overline x} \right)}^2} + {{\left( {{x_2} - \overline x} \right)}^2} + ... + {{\left( {{x_n} - \overline x} \right)}^2}}}{n} > 0\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} > 0\)
\(\Rightarrow\) Các số đo độ phân tán đều không âm
\(\Rightarrow\) (5) Đúng.