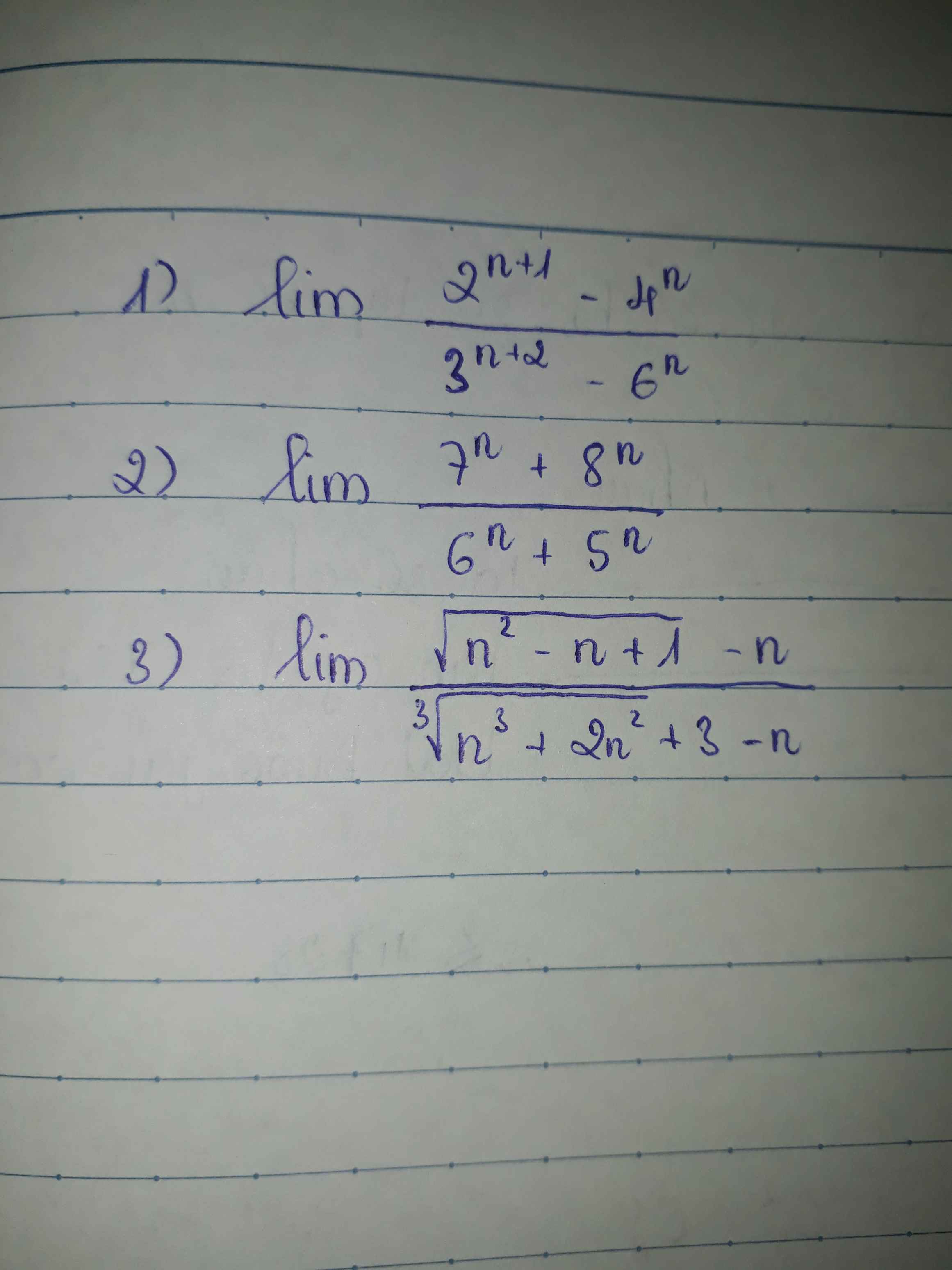\(\lim\dfrac{2^{n+1}-4^n}{3^{n+2}-6^n}=\lim\dfrac{2.2^n-4^n}{9.3^n-6^n}=\lim\dfrac{2\left(\dfrac{2}{6}\right)^n-\left(\dfrac{4}{6}\right)^n}{9\left(\dfrac{3}{6}\right)^n-1}=\dfrac{2.0-0}{9.0-1}=0\)
\(\lim\dfrac{7^n+8^n}{6^n+5^n}=\lim\dfrac{\left(\dfrac{7}{8}\right)^n+1}{\left(\dfrac{6}{8}\right)^n+\left(\dfrac{5}{8}\right)^n}=\dfrac{0+1}{0+0}=\dfrac{1}{0}=+\infty\)
Câu 3 là con số 3 dưới mẫu ở trong hay ngoài căn vậy nhỉ?
\(\lim\dfrac{\sqrt[]{n^2-n+1}-n}{\sqrt[3]{n^3+2n^2+3}-n}\)
\(=\lim\dfrac{\left(\sqrt[]{n^2-n+1}-n\right)\left(\sqrt[]{n^2-n+1}+n\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)}{\left(\sqrt[3]{n^3+2n^2+3}-n\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)\left(\sqrt[]{n^2-n+1}+n\right)}\)
\(=\lim\dfrac{\left(-n+1\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)}{\left(2n^2+3\right)\left(\sqrt[]{n^2-n+1}+n\right)}\)
\(=\lim\dfrac{\left(-1+\dfrac{1}{n}\right)\left(\sqrt[3]{\left(1+\dfrac{2}{n}+\dfrac{3}{n^3}\right)^2}+\sqrt[3]{1+\dfrac{2}{n}+\dfrac{3}{n^3}}+1\right)}{\left(2+\dfrac{3}{n^2}\right)\left(\sqrt[]{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1\right)}\)
\(=\dfrac{-1.\left(1+1+1\right)}{2.\left(1+1\right)}=-\dfrac{3}{4}\)
Ai giúp em câu này với ạ :((
