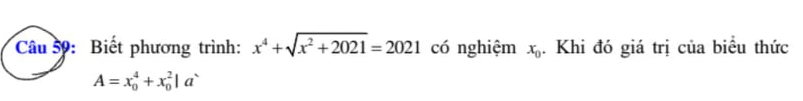Đặt \(\sqrt{x^2+2021}=a>0\Rightarrow2021=a^2-x^2\)
Pt trở thành:
\(x^4+a=a^2-x^2\)
\(\Leftrightarrow x^4-a^2+x^2+a=0\)
\(\Leftrightarrow\left(x^2+a\right)\left(x^2-a\right)+x^2+a=0\)
\(\Leftrightarrow\left(x^2+a\right)\left(x^2-a+1\right)=0\)
\(\Leftrightarrow x^2-a+1=0\)
\(\Leftrightarrow x^2-\sqrt{x^2+2021}+1=0\)
\(\Leftrightarrow x^2+1=\sqrt{x^2+2021}\)
\(\Leftrightarrow x^4+2x^2+1=x^2+2021\)
\(\Leftrightarrow x^4+x^2=2020\)
\(\Rightarrow A=2020\)
Đúng 0
Bình luận (0)
