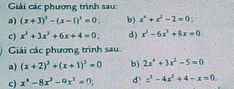Question

mn giúp em câu a với ạ

Answer 1

b)2x⁴+3x²-5=0

⇔2x⁴-2x³+2x³-2x²+5x²-5x+5x-5=0

⇔2x³(x-1)+2x²(x-1)+5x(x-1)+5(x-1)=0

⇔(x-1)(2x³+2x²+5x+5)=0

⇔(x-1)[2x²(x+1)+5(x+1)]=0

⇔(x-1)(x+1)(2x²+5)=0

Vì 2x²+5>0 nên pt trên tương đương:

(x-1)(x+1)=0

⇔x=1 hay x=-1

 

Answer 2

a) Áp dụng hằng đẳng thức: a³+b³=(a+b)(a²-ab+b²).

Answer 3

a)(x + 2)^3 + (x + 1)^3 = 0

<=> (x + 2 + x + 1)[(x + 1)^2 - (x + 1)(x + 2) + (x + 2)^2] = 0

<=> (2x + 3)(x^2 + 2x + 1 - x^2 - 3x - 2 + x^2 + 4x + 4) = 0

<=> (2x + 3)(x^2 + 3x + 3) = 0

<=> 2x + 3 = 0 hoặc x^2 + 3x + 3 = 0

<=> x = -3/2

b)2x^4 + 3x^2 - 5 = 0

<=> 2x^4 - 2x^3 + 2x^3 - 2x^2 + 5x^2 - 5x + 5x - 5 = 0

<=> 2x^3(x - 1) + 2x^2(x - 1) + 5x(x - 1) + 5(x - 1) = 0

<=> (x - 1)(2x^3 + 2x^2 + 5x + 5) = 0

<=> (x - 1)(x + 1)(2x^2 + 5) = 0

<=> (x^2 - 1)(2x^2 + 5) = 0

<=> x^2 - 1 = 0( vì 2x^2 + 5 > 0)

<=> x ∈ {-1,1}