1: |x+1|=2
=>x+1=2 hoặc x+1=-2
=>x=-3(nhận) hoặc x=1(loại)
Khi x=-3 thì \(B=\dfrac{-3-1}{-3+1}=\dfrac{-4}{-2}=2\)
2: \(A=\dfrac{x^2+x-3x+3+x-3}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x}{x+1}\)
3: C=A:B
\(=\dfrac{x}{x+1}:\dfrac{x-1}{x+1}=\dfrac{x}{x-1}\)
\(=\dfrac{x-1+1}{x-1}=1+\dfrac{1}{x-1}\)
Để C lớn nhất thi 1/x-1 lớn nhất
=>x-1=1
=>x=2










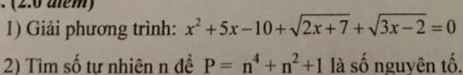


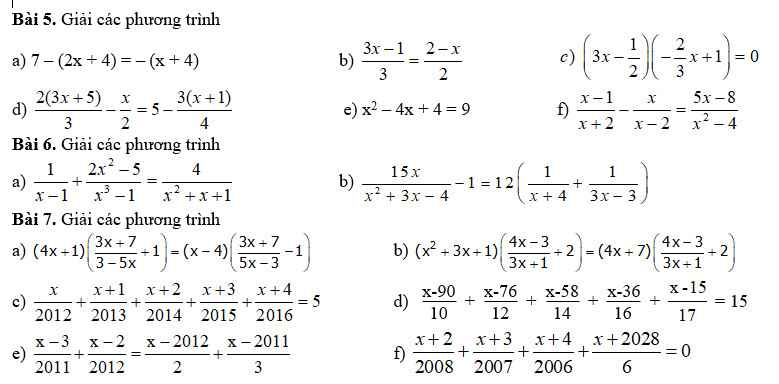 giúp mình gấp ạ
giúp mình gấp ạ





