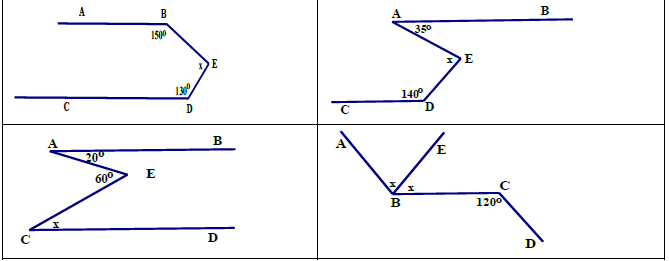
Bài 4:
Xét tam giác AHB vuông tại H:
\(\widehat{aAC}+\widehat{ABH}=90^0\Rightarrow\widehat{ABH}=90^0-40^0=50^0\)
Ta có: \(\widehat{ABH}+\widehat{HBb}+y=180^0\)
\(\Rightarrow y=180^0-50^0-90^0=40^0\)
Ta có: \(\widehat{BKC}=\widehat{ABH}=50^0\)(đối đỉnh)
Ta có: Aa//Dd, Aa⊥HK
=> Dd⊥HK\(\Rightarrow\widehat{BKD}=90^0\)
Xét tứ giác BKDC có:
\(\widehat{BKC}+\widehat{BCK}+\widehat{KDC}+\widehat{BKD}=360^0\)
\(\Rightarrow\widehat{KDC}=360^0-90^0-90^0-50^0=130^0\)
\(\Rightarrow x=\widehat{KDC}=130^0\)(so le trong do Ee//CD)