Bài 5:
Vì \(ab//cd\) và AB cắt ab và cd
Nên \(\widehat{bAB}+\widehat{ABd}=180^0\) (Hai góc trong cùng phía)
Mà Am là tia phân giác của \(\widehat{bAB}\)
\(\Rightarrow\widehat{BAm}=\dfrac{1}{2}.\widehat{bAB}\)
và Bn là tia phân giác của \(\widehat{ABd}\)
\(\Rightarrow\widehat{ABn}=\dfrac{1}{2}.\widehat{ABd}\)
Xét tam giác ABC, có:
\(\widehat{ABC}+\widehat{CAB}+\widehat{ACB}=180^0\)
Hay \(\widehat{ABn}+\widehat{BAm}+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.\widehat{ABd}+\dfrac{1}{2}.\widehat{BAb}+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(\widehat{ABd}+\widehat{BAb}\right)+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.180^0+\widehat{ACB}=180^0\)
\(\Leftrightarrow90^0+\widehat{ACB}=180^0\)
\(\Leftrightarrow\widehat{ACB}=180^0-90^0=90^0\)
Hay \(Am\perp Bn\left(đpcm\right)\)
Chúc bạn học tốt!
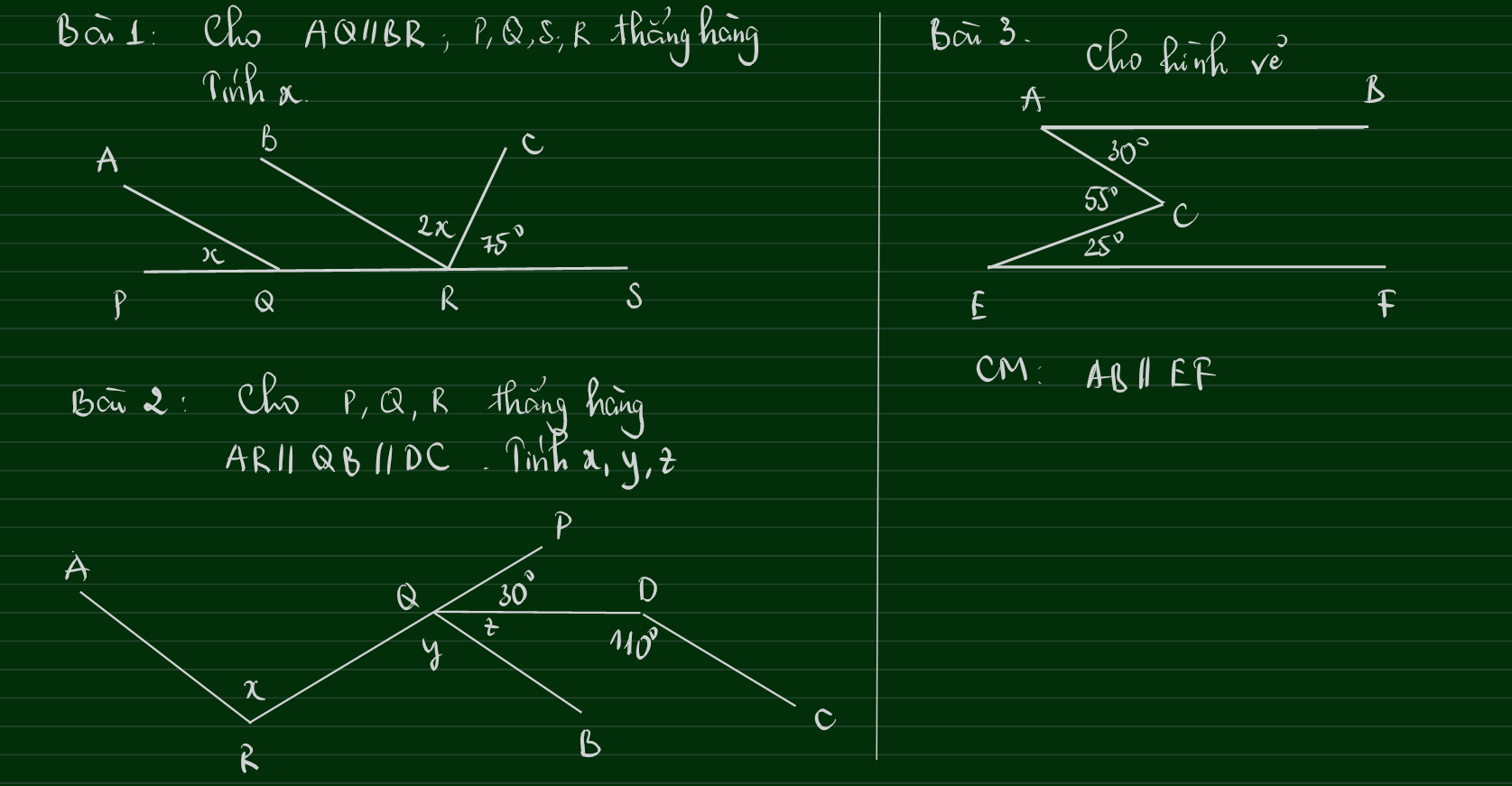
Bài 6:
Vì \(AB//CD\)
Nên \(\widehat{ABC}=\widehat{DCB}\) (Hai góc so le trong)
Mà \(\left\{{}\begin{matrix}\widehat{ABC}=x+x\\\widehat{DCB}=120^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{ABC}=2x\\\widehat{DCB}=120^0\end{matrix}\right.\)
\(\Leftrightarrow2x=120^0\)
\(\Leftrightarrow x=\dfrac{120^0}{2}=60^0\)
Vậy \(x=60^0\).
Chúc bạn học tốt!
Ta có Ob // Cd
=> ^BAb = ^CBA ( 2 góc so le trong )
mà Am là tia phân giác của ^BAb
và Bt là tia phân giác cũa ^CAB
=> ^BAm = ^ABt
mà ^BAm và ^ABt ở vị trí so le trong
=> Am // Bt (1)
Ta có Bt là tia phân giác của ^CBA
Bn là tia phân giác của ^ABd
mà ^CBA và ^ABd là hai góc kề bù
=> Bt \(\perp\) Bn (2)
Từ (1) và (2) => Am \(\perp\) Bn
2.
Ta có AB // CD
=> ^C = ^ABC = 120 độ ( 2 góc so le trong )
Mà BE là tia phân giác của ^ABC
=> x = 1/2 . ^ABC = 1/2 . 120độ = 60độ