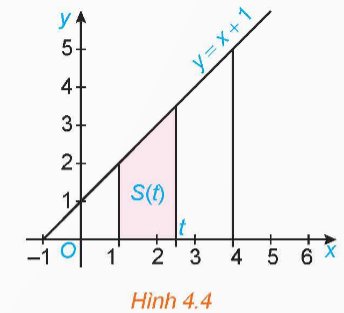
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≤ t ≤ 4) (H.4.4)
a) Tính diện tích S của T khi t = 4.
b) Tính diện tích S(t) của T khi t ∈ [1; 4].
c) Chứng minh rằng S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4] và diện tích S = S(4) – S(1).
a) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với trục hoành; B, C lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = 4\) với đường thẳng \(y = x + 1\).
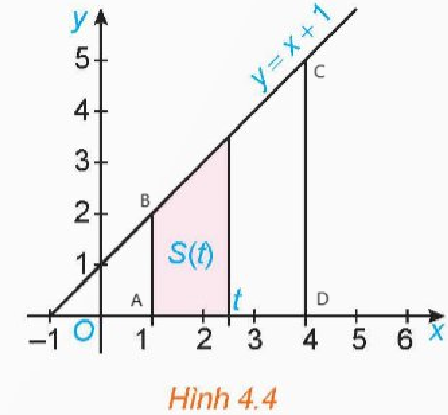
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {4;5} \right),D\left( {4;0} \right)\). Do đó, \(AB = 2,CD = 5,AD = 3\)
Diện tích hình thang ABCD là: \(S = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + 5} \right).3}}{2} = \frac{{21}}{2}\)
b) Gọi A, D lần lượt là giao điểm của các đường thẳng \(x = 1\), \(x = t\) với trục hoành, B, C lần lượt là giao điểm của đường thẳng \(x = 1\), \(x = t\) với đường thẳng \(y = x + 1\).
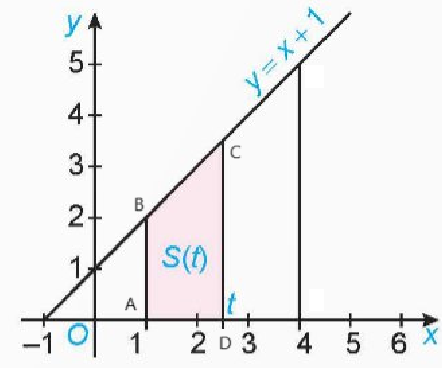
Khi đó, \(A\left( {1;0} \right),B\left( {1;2} \right),C\left( {t;t + 1} \right),D\left( {t;0} \right)\). Do đó, \(AB = 2,CD = t + 1,AD = t - 1\)
Diện tích hình thang ABCD là:
\(S\left( t \right) = \frac{{\left( {AB + CD} \right).AD}}{2} = \frac{{\left( {2 + t + 1} \right).\left( {t - 1} \right)}}{2} = \frac{{\left( {t + 3} \right)\left( {t - 1} \right)}}{2} = \frac{{{t^2} + 2t - 3}}{2}\)
c) Ta có: \(S'\left( t \right) = {\left( {\frac{{{t^2} + 2t - 3}}{2}} \right)'} = \frac{1}{2}\left( {2t + 2} \right) = t + 1 = f\left( t \right)\)
Do đó, S(t) là một nguyên hàm của hàm số \(f\left( t \right) = t + 1,t \in \left[ {1;4} \right]\).
Lại có: \(S\left( 4 \right) - S\left( 1 \right) = \frac{{{4^2} + 2.4 - 3}}{2} - \frac{{{1^2} + 2.1 - 3}}{2} = \frac{{21}}{2} - 0 = \frac{{21}}{2}\)
Suy ra: \(S = S\left( 4 \right) - S\left( 1 \right)\).


