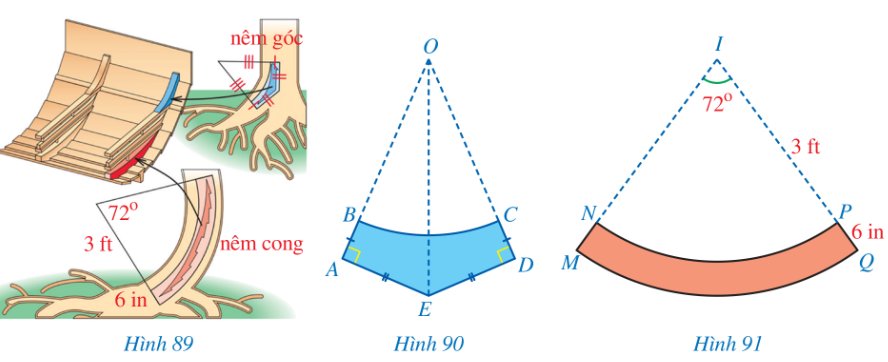
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikings sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt ABCD của nêm góc có dạng hai tam giác vuông OAE, ODE bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn OBC (Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt MNPQ của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.
a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48 cm, 1 in = 2,54 cm và làm tròn kết quả đến hàng đơn vị)?
b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?
a) Đổi \(3ft = 3.30,48 = 91,44cm\)
\(6in = 6.2,54 = 15,24 cm\)
+ Diện tích quạt tròn \(INP\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.91,44}^2}.72}}{{360}} \approx 5254\left( {c{m^2}} \right)\)
+ Diện tích quạt tròn \(IMQ\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{\left( {91,44 + 15,24)} \right)}^2}.72}}{{360}} \approx 7151\left( {c{m^2}} \right)\)
+ Diện tích của nêm cong là:
\(S = {S_{IMQ}} - {S_{INP}} \approx 7151 - 5254 \approx 1897\left( {c{m^2}} \right)\)
b) Diện tích nêm góc = diện tích 2 tam giác - diện tích hình quạt OBC.
\(S_{2\Delta} = 2.\frac{1}{2} OA.OE = OA.OE\)
\(S_{OBC} = \frac{\pi.OB^2.\widehat{BOC}}{360}\)
\(S_{nêm\;góc} = OA.AE - \frac{\pi.OB^2.\widehat{BOC}}{360}\)
Vậy để tính được diện tích của nêm góc cần biết: góc \(BOC\), cạnh OB, OA (hoặc AE).


