Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15$ (cm)
$CC'=\sqrt{BC'^2-BC^2}=\sqrt{17^2-15^2}=8$ (cm)
Diện tích xung quanh hình lăng trụ là:
$(9+12+15).8=288$ (cm2)
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=4cm, BC=5cm, CC’=6cm, tam giác ABC vuông tại A. tính diện tích xung quanh và thể tích của hình lăng trụ
Cho hình lăng trụ đứng .Biết MQ=5cm, MN=3cm, NP=9cm, NM=4cm.
a,Tính độ dài cạnh còn lại của đáy MNPQ.
b,Tính diện tích xung quanh của lăng trụ đứng.
c,Tính diện tích toàn phần của lăng trụ đứng.
d,Thể tích của lăng trụ đứng.
Nhanh giúp mình nha.Thanks you những bạn làm giúp mình^_^
Người ta cắt một khối gỗ có dạng một hình lập phương như hình 124 (cắt theo mặt \(ACC_1A_1\) ) và được hai lăng trụ đứng
a) Đáy của lăng trụ đứng nhận được là tam giác vuông, tam giác cân hay là tam giác đều ?
b) Các mặt bên của mỗi lăng trụ đứng nhận được có phải tất cả đều là hình vuông hay không ?
Diện tích xung quanh của hình lăng trụ đứng là "p.h" hay "2p.h" vậy?
Đáy của lăng trụ đứng là một hình thang cân có các cạnh b = 11mm, a = 15mm và chiều cao \(h_r=7mm\) (h.127). Chiều cao của lăng trụ là \(h=14mm\).
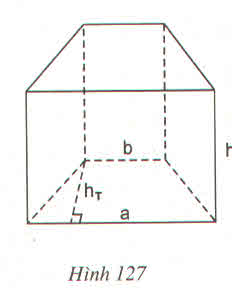
Tính diện tích xung quanh của lăng trụ ?
một hình lăng trụ đứng có đáy là tam giác vuông.độ dài 2 cạnh góc đáy là 6cm,8cm. chiều cao là 12cm, tính dt toàn phần
Tính diện tích toàn phần hình lăng trụ đứng tam giác có các cạnh đáy và cạnh bên đều = 2cm
Tính diện tích xung quanh của hình lăng trụ đứng ABCD.A'B'C'D',biết AA'=6 cm,ABCD là hình chữ nhật có AB=5cm,AD=12cm
Một lăng trụ đứng lục giác đều có độ dài cạnh đáy là 6cm, chiều cao của lăng trụ là 10cm. Diện tích toàn phần của lăng trụ đó là (đơn vị \(cm^2\))
(A) \(180+54\sqrt{3}\)
(B) \(180+108\sqrt{3}\)
(C) \(360+54\sqrt{3}\)
(D) \(360+108\sqrt{3}\)
Hãy chọn kết quả đúng ?
