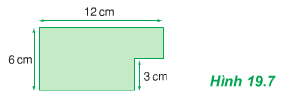
Vì bản phẳng, mỏng, đồng chất nên ta có thể coi nó gồm hai tấm ghép lại.
- Tấm thứ nhất có dạng hình chữ nhật, dài $9 cm$, rộng $6 cm$; trọng lực là $\overrightarrow{P}_1$ đặt tại $G_1$
- Tấm thứ hai có dạng hình vuông, mỗi cạnh $3cm$; trọng lực là $\overrightarrow{P}_2$ đặt tại $G_2$.
Như vậy bản phẳng cần xét có trọng lực là $\overrightarrow{P}=\overrightarrow{P}_1+\overrightarrow{P}_2$ và đặt tại $G$.
Theo quy tắc hợp lực song song: $\frac{P_1}{P_2}=\frac{d_2}{d_1}=\frac{GG_2}{GG_1}$
Mặt khác: $\frac{P_1}{P_2}=\frac{S_1}{S_2}=\frac{6.9}{3.3}=6\Rightarrow GG_2=6.GG_1 (1)$
Dựa vào hình vẽ ta có: $G_1G_2=\sqrt{6^2+1,5^2}=6,18cm (2)$
Từ $(1)$ và $(2)$, suy ra $GG_1=0,88 cm$
Vậy vị trí của $G$ nằm trong khoảng $G_1G_2$ và cách $G-1$ là $0,88 cm$