Question

Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S₁ là diện tích hình phẳng giới hạn bởi d, trục hoành và trục tung, S₂ là diện tích hình phẳng giới hạn bởi d, trục hoành và đường thẳng x = 5 (Hình 1).

a) Tính S₁ và so sánh với \(\int\limits^5_3f\left(x\right)dx\).

b) Tính S₂ và so sánh với \(\int\limits^5_3f\left(x\right)dx\).

c) So sánh \(\int\limits^5_0\left|f\left(x\right)\right|dx\) với S₁ + S₂.

Answer 1

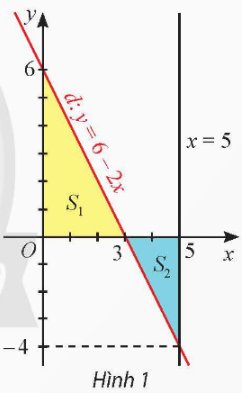
a) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:

\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).

Ta có \(\int\limits_0^3 {f\left( x \right)dx}  = \int\limits_0^3 {\left( {6 - 2x} \right)dx}  = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).

Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)

b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:

\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).

Ta có \(\int\limits_0^3 {f\left( x \right)dx}  = \int\limits_3^5 {\left( {6 - 2x} \right)dx}  = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 =  - 4\).

Như vậy \({S_2} =  - \int\limits_3^5 {f\left( x \right)dx} \)

c) Ta có:

\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx}  = \int\limits_0^5 {\left| {6 - 2x} \right|dx}  = \int\limits_0^3 {\left| {6 - 2x} \right|dx}  + \int\limits_3^5 {\left| {6 - 2x} \right|dx}  = \int\limits_0^3 {\left( {6 - 2x} \right)dx}  + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)

\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)

Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx}  = 13 = {S_1} + {S_2}\).