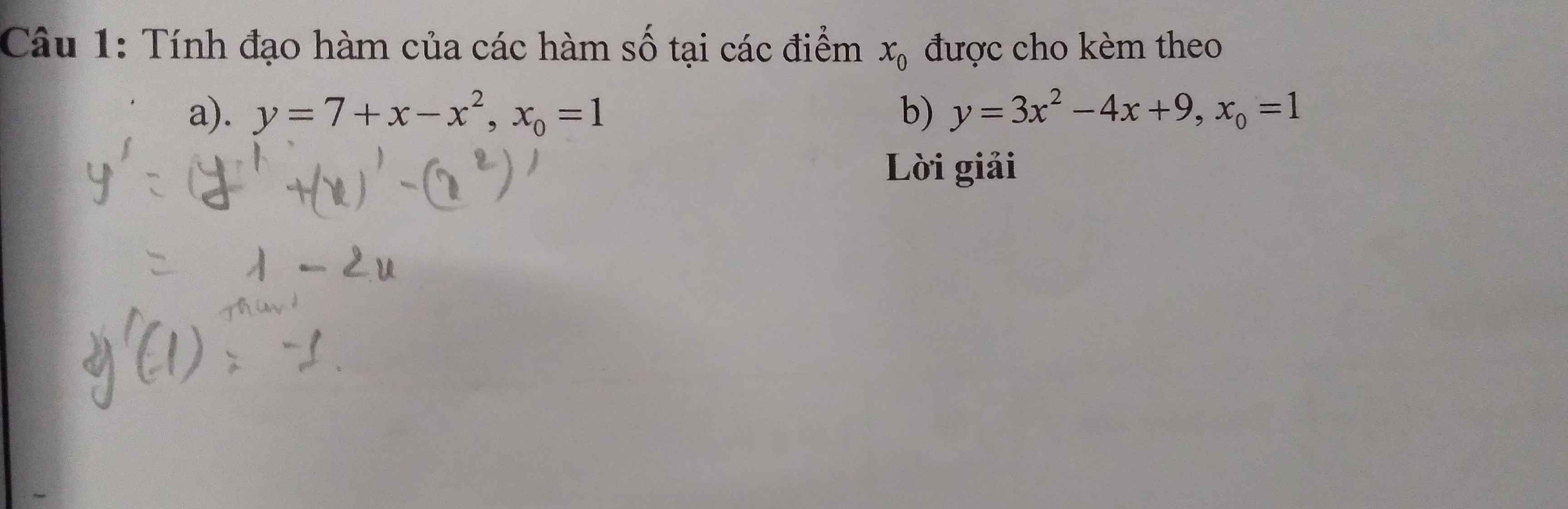Lời giải:
a) $y=\frac{3}{x^2}-(x)^{\frac{1}{2}}+\frac{2}{3}(x)^{\frac{3}{2}}$
$y'=\frac{-3(x^2)'}{x^4}-\frac{1}{2}x^{\frac{-1}{2}}+\frac{2}{3}.\frac{3}{2}.x^{\frac{1}{2}}$
$=\frac{-6}{x^3}-\frac{1}{2\sqrt{x}}+x$
b)
$y=(x+1)^{\frac{1}{2}}[(x)^{\frac{-1}{2}}-1)$
$y'=\frac{1}{2}(x+1)^{\frac{-1}{2}}[(x)^{\frac{-1}{2}}-1)+(x+1)^{\frac{1}{2}}[\frac{-1}{2}x^{-\frac{3}{2}}]=\frac{1}{2\sqrt{x+1}}(\frac{1}{\sqrt{x}}-1)-\frac{1}{2}\sqrt{x+1}.\frac{1}{\sqrt{x^3}}$
c)
\(y'=\frac{[(x+1)^2]'(x-1)^3-(x+1)^2[(x-1)^3]'}{(x-1)^6}=\frac{(2x+2)(x-1)^3-3(x-1)^2(x+1)^2}{(x-1)^6}\)
\(=\frac{(2x+2)(x-1)-3(x+1)^2}{(x-1)^4}=\frac{-(x+1)(x+5)}{(x-1)^4}\)
d)
\(y=1+(1-2x)^{\frac{3}{2}}\)
\(y'=\frac{3}{2}(1-2x)'(1-2x)^{\frac{3}{2}-1}=\frac{3}{2}(-2)(1-2x)^{\frac{1}{2}}=-3\sqrt{1-2x}\)
e)
$y=(x-2)(x^2+3)^{\frac{1}{2}}=(x-2)'(x^2+3)^{\frac{1}{2}}+(x-2)\frac{1}{2}.(x^2+3)'(x^2+3)^{\frac{1}{2}-1}$
$=\sqrt{x^2+3}+\frac{x(x-2)}{\sqrt{x^2+3}}=\frac{2x^2-2x+3}{\sqrt{x^2+3}}$
f)
\(y=\frac{(4x+1)'\sqrt{x^2+2}-(4x+1)\sqrt{x^2+2}'}{x^2+2}=\frac{4\sqrt{x^2+2}-\frac{x(4x+1)}{\sqrt{x^2+2}}}{x^2+2}\)
\(=\frac{8-x}{\sqrt{(x^2+2)^3}}\)







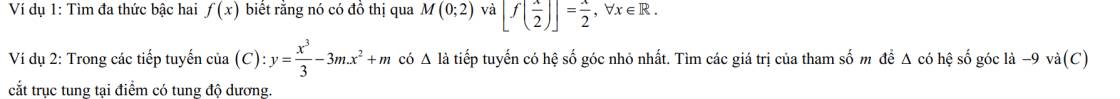 MỌI NGƯỜI GIÚP MÌNH HAI CÂU NÀY VỚI Ạ
MỌI NGƯỜI GIÚP MÌNH HAI CÂU NÀY VỚI Ạ