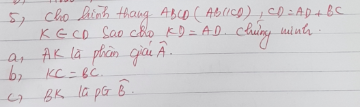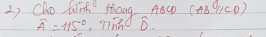a,△ABC vuông cân tại A
⇒\(\widehat{ACB}=45độ\)
△EAC vuông cân tại E
⇒\(\widehat{EAC}=45độ\)
Suy ra : \(\widehat{EAC}=\widehat{ACB}\)
⇒AE // BC ( vì có cặp góc ở vị trí sole trong bằng nhau )
nên tứ giác AECB là hình thang có \(\widehat{E}=90độ\) . Vậy AECB là hình thang vuông
b,\(\widehat{E}=\widehat{ECB}=90độ\) , \(\widehat{B}=45độ\)
\(\widehat{B}+\widehat{EAB}=180độ\) ( hai góc trong cùng phía bù nhau )
⇒\(\widehat{EAB}=180-\widehat{B}=180-45=135độ\)
△AEC vuông tại E. Theo định lỳ PITAGO ta có :
\(AB^2+AC^2=BC^2,màAB=AC\left(gt\right)\)
⇒\(2AB^2=BC^2=2^2=4\)
\(AB^2=2\Rightarrow AB=\sqrt{2}\left(cm\right)\Rightarrow AC=\sqrt{2}9cm\)
△AEC vuông tại E .Theo định lý PITAGO ta có :
\(EA^2+EC^2=AC^2,màEA=EC\left(gt\right)\)
⇒\(2EA^2=AC^2=2\)
\(EA^2=1\)
⇒\(EA=1\left(cm\right)\Rightarrow EC=1\left(cm\right)\)