Bài 1:
a, Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đths cần tìm
Vì (d) đi qua A(1;2) và B(-2;-5) nên \(\left\{{}\begin{matrix}a+b=2\\-2a+b=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{7}{3}\\b=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy đths cần tìm là \(\left(d\right):y=\dfrac{7}{3}x-\dfrac{1}{3}\)
b, Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đths cần tìm
Vì (d) đi qua M(3;2) và \(\left(d\right)//y=2x+5\) nên \(\left\{{}\begin{matrix}3a+b=2\\a=2\\b\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-4\end{matrix}\right.\)
Vậy đths cần tìm là \(\left(d\right):y=2x-4\)
c, Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đths cần tìm
Vì (d) đi qua N(1;-5) và \(\left(d\right)\perp\left(d'\right)=-2x+3\) nên \(\left\{{}\begin{matrix}a+b=-5\\-2a=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-\dfrac{11}{2}\end{matrix}\right.\)
Vậy đths cần tìm là \(\left(d\right):y=\dfrac{1}{2}x-\dfrac{11}{2}\)
e, Gọi \(\left(d''\right):y=ax+b\left(a\ne0\right)\) là đths cần tìm
PTHDGD (d) và (d') là \(2x-3=7-3x\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\)
Để (d'') cần tìm đồng quy với (d) và (d') thì \(A\left(2;1\right)\in\left(d''\right)\)
Mà \(E\left(0;4\right)\in\left(d''\right)\Leftrightarrow\left\{{}\begin{matrix}2a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{3}{2}\\b=4\end{matrix}\right.\)
Vậy đths cần tìm là \(\left(d''\right):y=-\dfrac{3}{2}x+4\)
g, Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đths cần tìm
Vì (d) đi qua K(6;-4) nên \(6a+b=-4\Leftrightarrow b=-4-6a\)
Gọi A,B lần lượt là giao điểm của (d) với Ox,Oy
Khi đó \(A\left(x_1;0\right);B\left(0;y_1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=ax_1+b\\y_1=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{b}{a}\\y_1=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\left(-\dfrac{b}{a};0\right)\\B\left(b;0\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}OA=\left|-\dfrac{b}{a}\right|\\OB=\left|b\right|\end{matrix}\right.\)
Gọi H là hình chiếu của O trên \(\left(d\right)\Leftrightarrow OH=\dfrac{12}{5}\)
Áp dụng HTL vào tam giác AOB vuông tại O, đường cao OH:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\Leftrightarrow\dfrac{1}{\left|-\dfrac{b}{a}\right|^2}+\dfrac{1}{\left|b\right|^2}=\dfrac{25}{144}\\ \Leftrightarrow\dfrac{1}{\left(\dfrac{6a+4}{a}\right)^2}+\dfrac{1}{\left(6a+4\right)^2}=\dfrac{25}{144}\\ \Leftrightarrow\dfrac{a^2+1}{\left(6a+4\right)^2}=\dfrac{25}{144}\\ \Leftrightarrow144a^2+144=25\left(6a+4\right)^2\\ \Leftrightarrow144a^2+144=900a^2+1200a+400\\ \Leftrightarrow756a^2+1200a+256=0\\ \Leftrightarrow189a^2+300a+64=0\\ \Leftrightarrow\left(63a+16\right)\left(3a+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=-\dfrac{16}{63}\Rightarrow b=-\dfrac{52}{21}\\a=-\dfrac{4}{3}\Rightarrow b=4\end{matrix}\right.\)
Vậy đths cần tìm là \(\left(d\right):y=-\dfrac{16}{63}x-\dfrac{52}{21}\) và \(\left(d\right):y=-\dfrac{4}{3}x+4\)
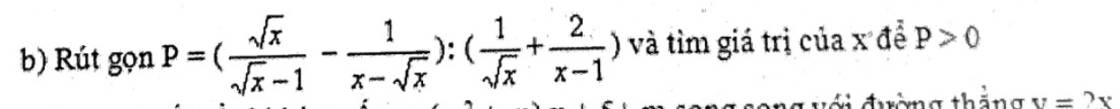Tìm giúp em giá trị của x ạ. E xin cảm ơn
