7) Áp dụng BĐT Cauchy-Schwarz, ta có
\(\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c+3}\ge\dfrac{9}{6}=\dfrac{3}{2}\)
\(Min_B=\dfrac{3}{2}\) khi a=b=c
5) Áp dụng BĐT Bunyakovsky, ta có:
\(\left(4x+5y\right)^2\le\left(4^2+5^2\right)\left(x^2+y^2\right)\)
\(x^2+y^2\le\dfrac{\left(4x+5y\right)^2}{4^2+5^2}=\dfrac{625}{41}\)
Đẳng thức xảy ra khi









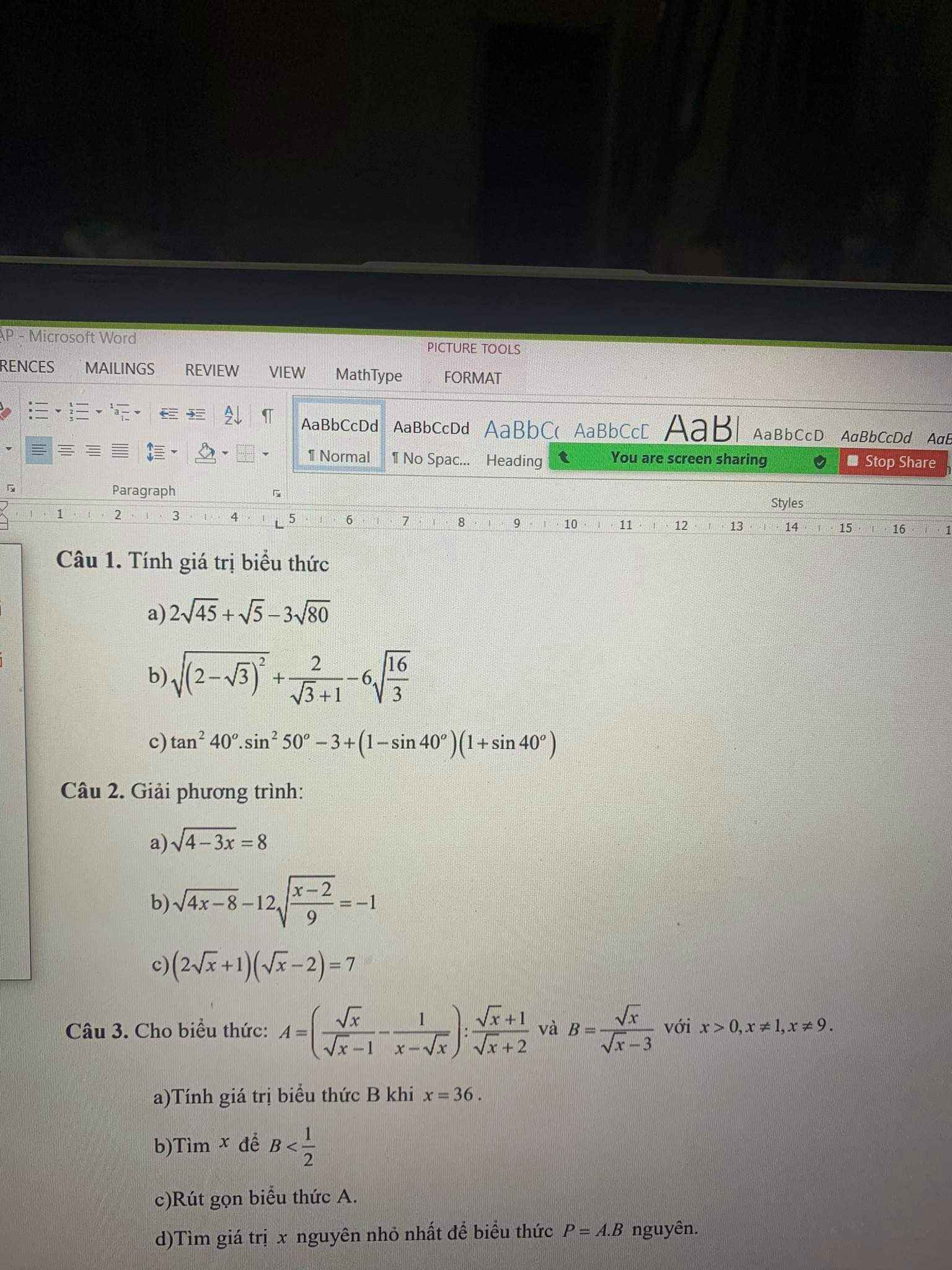



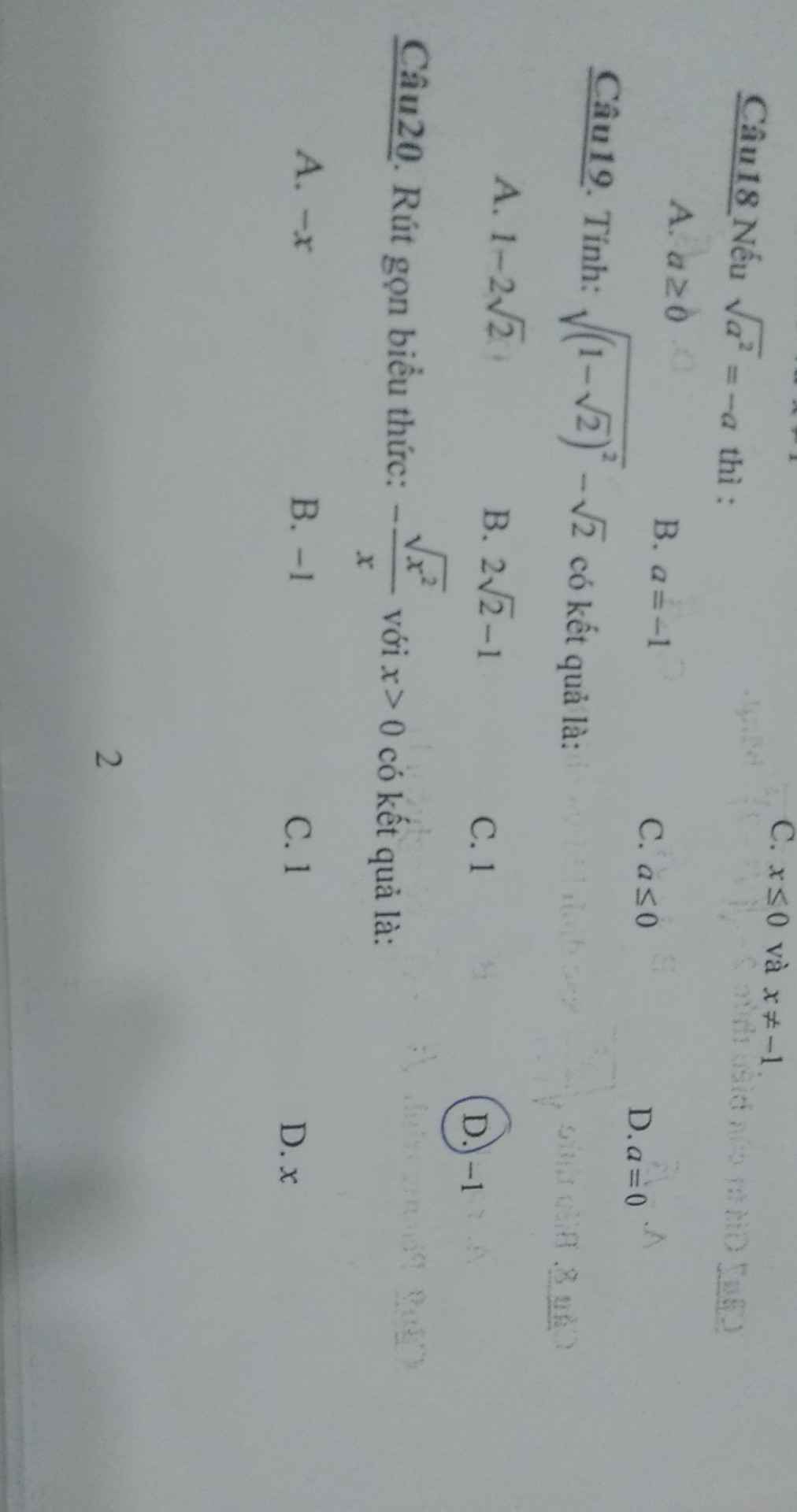


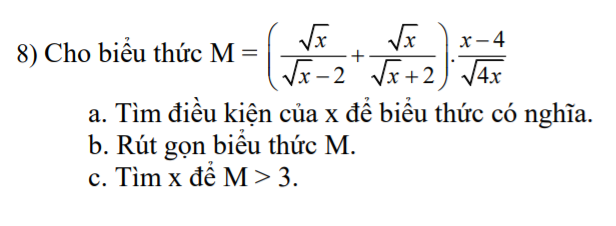

 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !