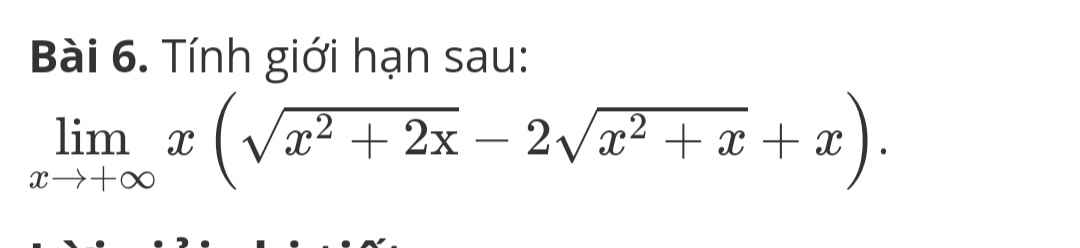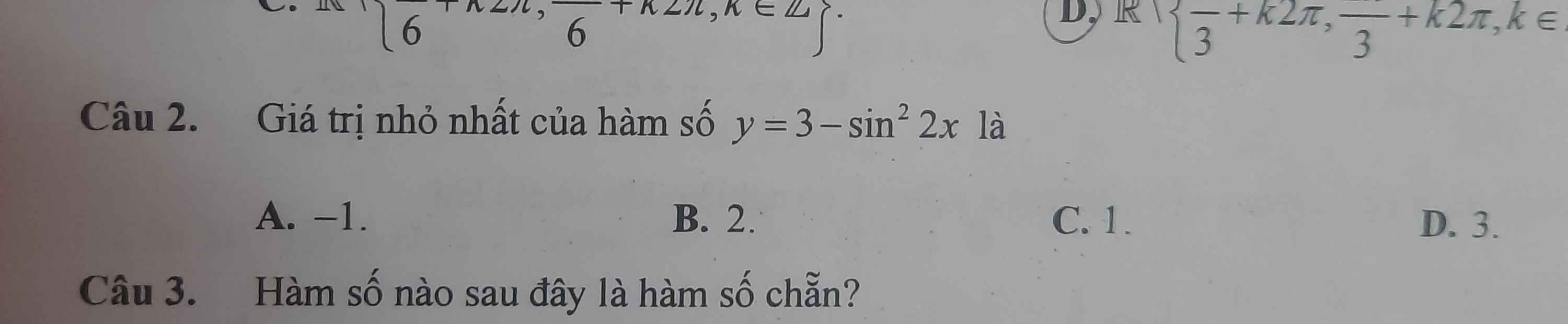\(2sin^2x-3sinx+1=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) (\(k\in Z\)) (I)
Có \(0\le x< \dfrac{\pi}{2}\)\(\Leftrightarrow\left[{}\begin{matrix}0\le\dfrac{\pi}{2}+k2\pi< \dfrac{\pi}{2}\\0\le\dfrac{\pi}{6}+k2\pi< \dfrac{\pi}{2}\\0\le\dfrac{5\pi}{6}+k2\pi< \dfrac{\pi}{2}\end{matrix}\right.\)(\(k\in Z\))
\(\Leftrightarrow\left[{}\begin{matrix}0\le\dfrac{1}{2}+2k< \dfrac{1}{2}\\0\le\dfrac{1}{6}+2k< \dfrac{1}{2}\\0\le\dfrac{5}{6}+2k< \dfrac{1}{2}\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{4}\le k< 0\left(1\right)\\-\dfrac{1}{12}\le k< \dfrac{1}{6}\left(2\right)\\-\dfrac{5}{12}\le k< -\dfrac{1}{6}\left(3\right)\end{matrix}\right.\)(\(k\in Z\))
Do k nguyên, từ (1) và (3) \(\Rightarrow k\in\varnothing\)
Từ (2)\(\Rightarrow k=0\)\(\Rightarrow x=\dfrac{\pi}{6}+0.2\pi=\dfrac{\pi}{6}\)
Ý C
(Hoặc sau khi bạn làm đến đoạn số (I),bạn vẽ đường tròn lượng giác ra sẽ tìm được x)