\(\sqrt{x-y+z}=\sqrt{x}-\sqrt{y}+\sqrt{z}\\ \Leftrightarrow x-y+z=x+y+z-2\sqrt{xy}-2\sqrt{yz}+2\sqrt{xz}\\ \Leftrightarrow2y-2\sqrt{xy}-2\sqrt{yz}+2\sqrt{xz}=0\\ \Leftrightarrow y-\sqrt{xy}-\sqrt{yz}+\sqrt{xz}=0\\ \Leftrightarrow\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)-\sqrt{z}\left(\sqrt{y}-\sqrt{x}\right)=0\\ \Leftrightarrow\left(\sqrt{y}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{x}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}y=z\\y=x\end{matrix}\right.\Leftrightarrow x=y=z\)
Chương I - Căn bậc hai. Căn bậc ba
Đúng 4
Bình luận (0)
Các câu hỏi tương tự
Anh chị giúp em câu này với, Toán lớp 9 .Em cảm ơn nhiều ạ.Cảm ơn anh chị
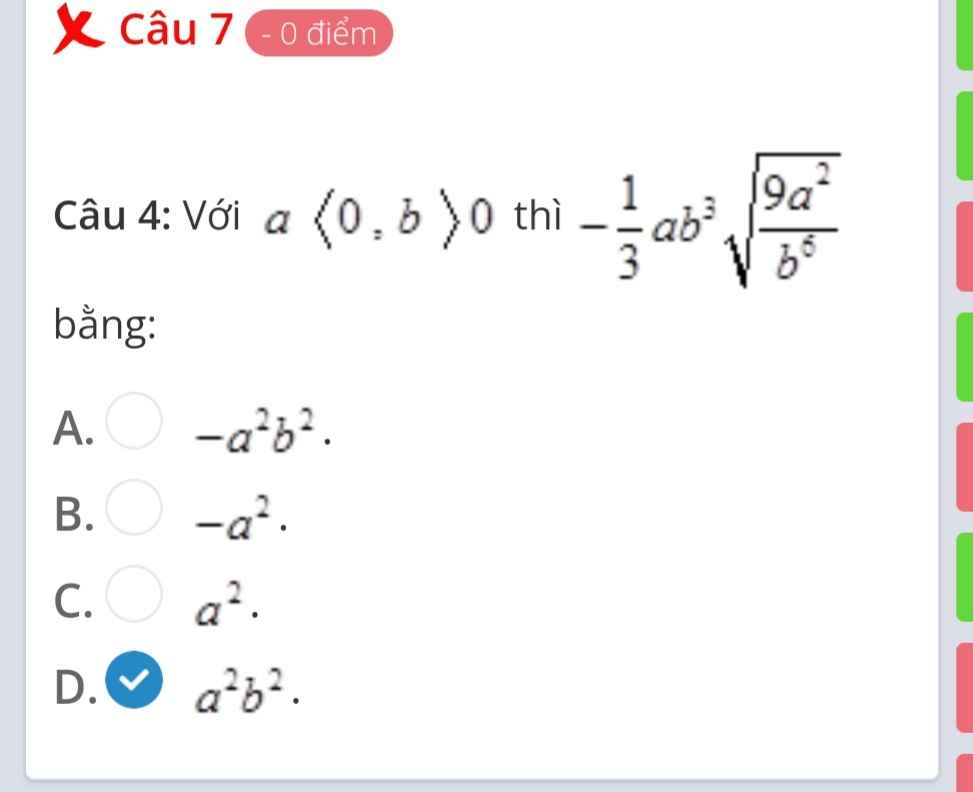
Giúp em câu 4b với , em cảm ơn

Em cảm ơn.
So sánh căn 7 -2 và 3 - căn 7 Mn lm ơn giúp em vs ạ ! Chiều em phải nộp rồi ạ ! Em cảm ơn
giúp em bài 1 với ạ,em cảm ơn

Em cảm ơn ạ.
Làm rõ ràng hộ em ạ, em cảm ơn <3
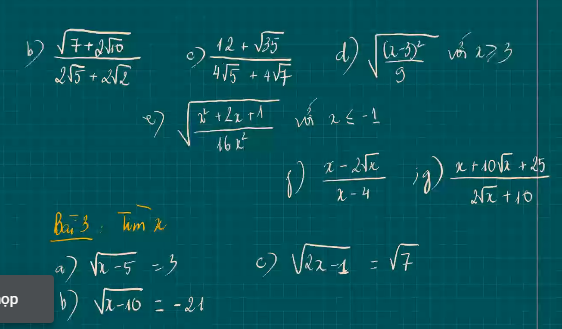
Giải giúp em vs ạ. Em xin cảm ơn o(︶︿︶)o
Giúp em hai bài này với ạ! Em cảm ơn rất nhiều!











