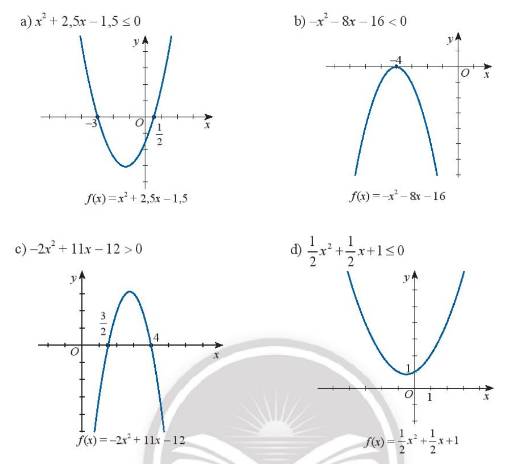
a) Dựa vào đồ thị ta thấy \({x^2} + 2,5x - 1,5 \le 0\) khi x thuộc đoạn \(\left[ { - 3;\frac{1}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} + 2,5x - 1,5 \le 0\) là \(\left[ { - 3;\frac{1}{2}} \right]\)
b) Dựa vào đồ thị ta thấy \( - {x^2} - 8x - 16 < 0\) với mọi x khác \( - 4\)
Vậy nghiệm của bất phương trình \( - {x^2} - 8x - 16 < 0\) là \(\mathbb{R}\backslash \left\{ { - 4} \right\}\)
c) Dựa vào đồ thị ta thấy \( - 2{x^2} + 11x - 12 > 0\) khi x thuộc khoảng \(\left( {\frac{3}{2};4} \right)\)
Vậy nghiệm của bất phương trình \( - 2{x^2} + 11x - 12 > 0\) là \(\left( {\frac{3}{2};4} \right)\)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức \(f\left( x \right) = \frac{1}{2}{x^2} + \frac{1}{2}x + 1\) nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình \(\frac{1}{2}{x^2} + \frac{1}{2}x + 1 \le 0\) vô nghiệm.